A dparticle of mas m moving with speed u collides elastically with a sphere of radius R and same mass at rest, at an impact parameter d. Find
(a) Angle between their final velocities and
(b) Magpitude of their final velocities.

Video Solution

Text Solution

Verified by Experts

As the collision is perfectly elastic and masses of both the particles are same thus their velocity vectors should b e exchanged along the line impact.
Thus $v_{2} = u cos θ and v_{3} = 0$
Now id we focus on the particle along there is no force on it parpendicular to the line of impact.
Thus its velocity does not change in this directin and hence.
$v_{1} = u sin θ$
Now, from geometry,
$sin θ = \frac{d}{R}$
$cos θ = \sqrt{1 - \frac{d^{2}}{R^{2}}}$
$\Rightarrow v_{2} = \frac{u}{R} \sqrt{R^{2} - d^{2}}$
$v_{1} = \frac{u d}{R}$
$v_{3} = 0$

|

Updated on:21/07/2023

Class 12 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An object of mass $M_{1}$ moving horizontally with speed u collides elastically with another object of mass $M_{2}$ at rest. Select correct statement.

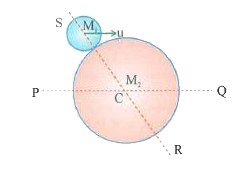AThe momentum of system is conserved only in direction PQ
BMomentum of $M_{1}$ is conserved in direction perpendicular to SR
CMomentum of $M_{2}$ will change in direction normal to CR
DAll of these
Question 2 - Select One
A body of mass $\frac{m}{2}$ moving with velocity $v_{0}$ collides elastically with another mass of $\frac{m}{3}$ . Find % change in KE of first body
A32
B96
C34
D80
Question 3 - Select One
A smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
A $\frac{2 u M}{m}$
B $\frac{2 μ M}{M}$
C $\frac{2 u}{1 + \frac{m}{M}}$
D $\frac{2 u}{1 + \frac{M}{m}}$

AAKASH INSTITUTE-WORK, ENERGY AND POWER-Assignment (SECTION - D)

Home
Ask Doubt
Profile