Question

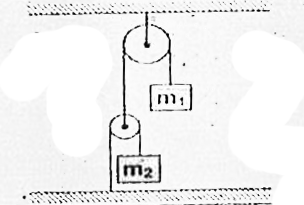
In an atwood machine the two blocks have massess $1kg$ and $3kg$. The pulley is massless and frictionless and string is light. The acceleration of the centre of mass (in $m/s^2$) of this system is $0.5x$. Find the value of $x$.

Explanation

To solve the problem of the Atwood machine with masses of 1 kg and 3 kg, we will follow these steps:

Step 1: Identify the forces acting on each mass
- For the 3 kg mass (m1):
- Weight (W1) = m1 * g = 3 kg * 10 m/s² = 30 N (downward)
- For the 1 kg mass (m2):
- Weight (W2) = m2 * g = 1 kg * 10 m/s² = 10 N (downward)

Step 2: Write the equations of motion for each mass
- For the 3 kg mass (m1):
\( m1 \cdot g - T = m1 \cdot a \quad \text{(1)} \)
where T is the tension in the string and a is the acceleration of the system.

- For the 1 kg mass (m2):
\( T - m2 \cdot g = m2 \cdot a \quad \text{(2)} \)

Step 3: Substitute the values into the equations
From equation (1):
\( 30 - T = 3a \quad \text{(3)} \)

From equation (2):
\( T - 10 = 1a \quad \text{(4)} \)

Step 4: Solve the equations simultaneously
Add equations (3) and (4):
\( (30 - T) + (T - 10) = 3a + 1a \)
This simplifies to:
\( 30 - 10 = 4a \)
\( 20 = 4a \)
\( a = \frac{20}{4} = 5 \, \text{m/s}^2 \)

Step 5: Calculate the acceleration of the center of mass (ACM)
The total mass of the system (M) is:
\( M = m1 + m2 = 3 \, \text{kg} + 1 \, \text{kg} = 4 \, \text{kg} \)

The acceleration of the center of mass (ACM) can be calculated using the formula:
\( A_{CM} = \frac{\Sigma m_i a_i}{\Sigma m_i} \)
Where \(a_i\) is the acceleration of each mass. Since the 1 kg mass is moving upward with acceleration \(5 \, \text{m/s}^2\) and the 3 kg mass is moving downward with the same acceleration:
\( A_{CM} = \frac{(1 \cdot 5) + (3 \cdot -5)}{4} = \frac{5 - 15}{4} = \frac{-10}{4} = -2.5 \, \text{m/s}^2 \)
The negative sign indicates that the center of mass is accelerating downward.

Step 6: Relate the acceleration of the center of mass to the given expression
According to the problem, the acceleration of the center of mass is given as \(0.5x\):
\( 0.5x = 2.5 \)

Step 7: Solve for x
To find the value of \(x\):
\( x = \frac{2.5}{0.5} = 5 \)

Final Answer
The value of \(x\) is \(5\).