The gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
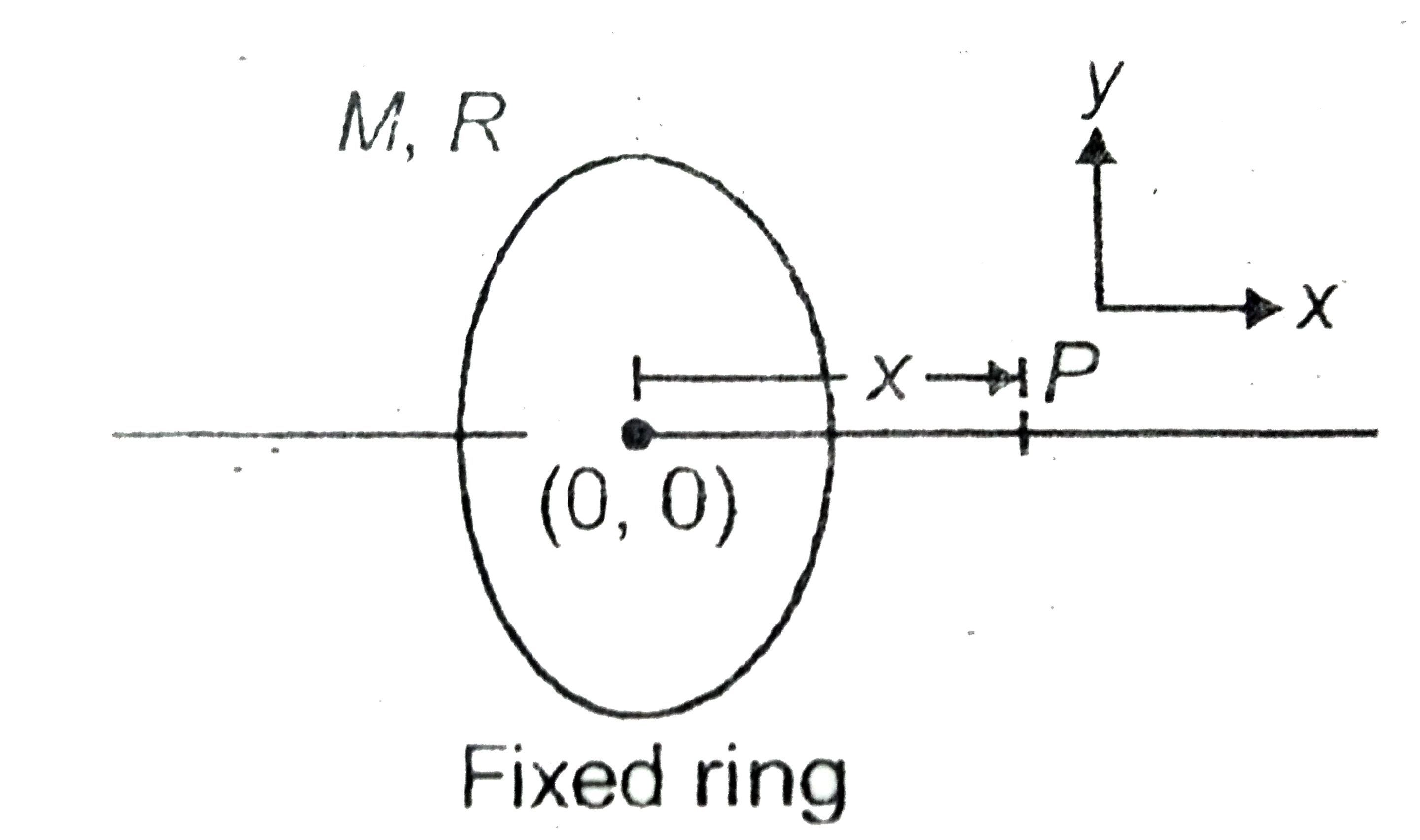
If the point mass m placed at the centre of ring and given a velocity v0 such that point mass escapes from the gravitational field of ring. Then v0 is
√32GMR
√GM2R
√2GMR
√GMR
The correct Answer is:C
Step by step video & image solution for The gravitational force vec(F) upon an object of mass m placed in external gravitational field vec(E )_("ext") is given by vec(F)=m vec(E )_("ext"). Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction. If the point mass m placed at the centre of ring and given a velocity v_(0) such that point mass escapes from the gravitational field of ring. Then v_(0) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -E (Assertion - Reason Type Questions)
14 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -F (Matrix - Match Type Questions)
9 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -C (Objective Type Questions (More than one option are correct))
11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
The gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
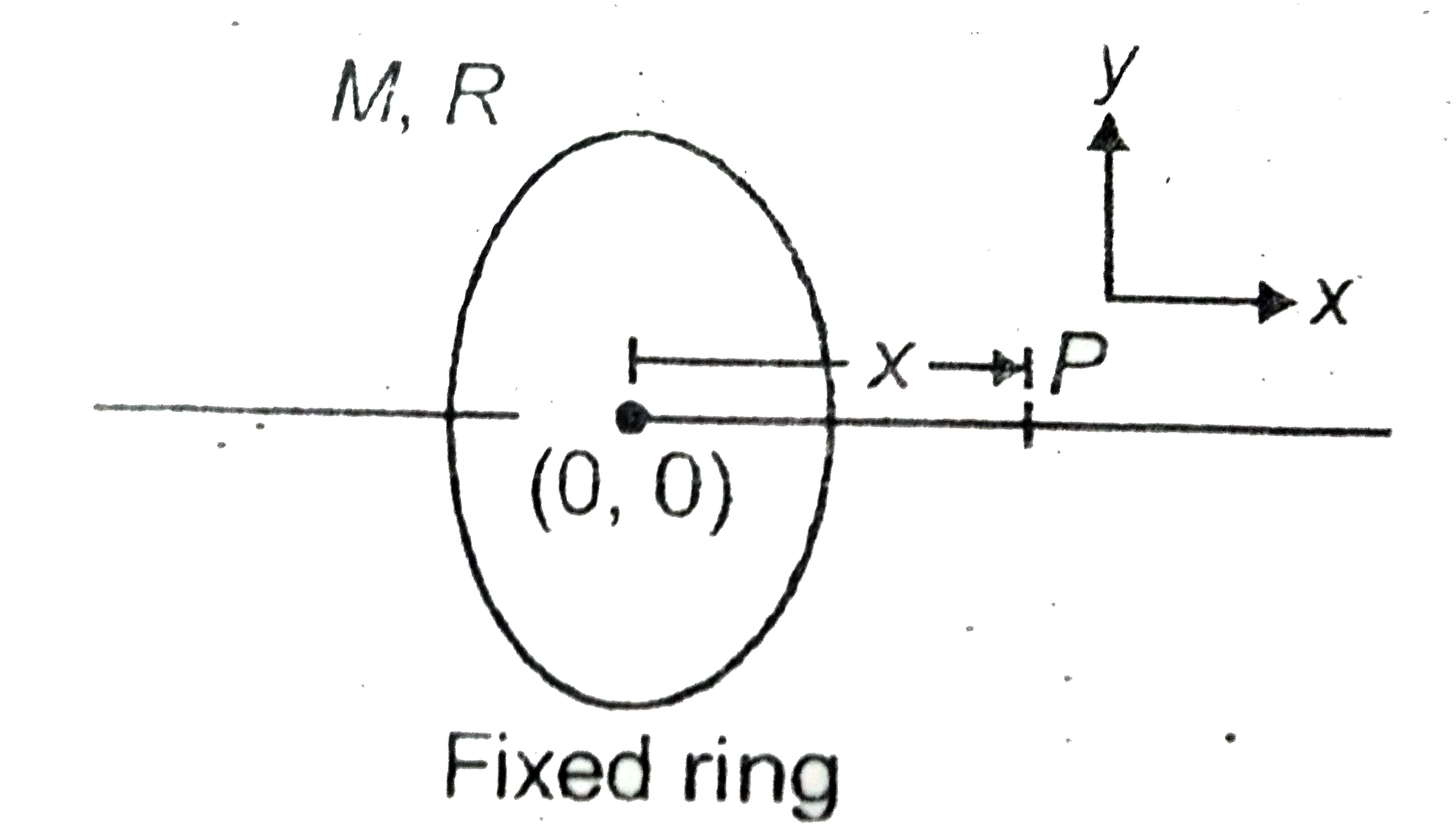
The gravitational field is zero at x equal to
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
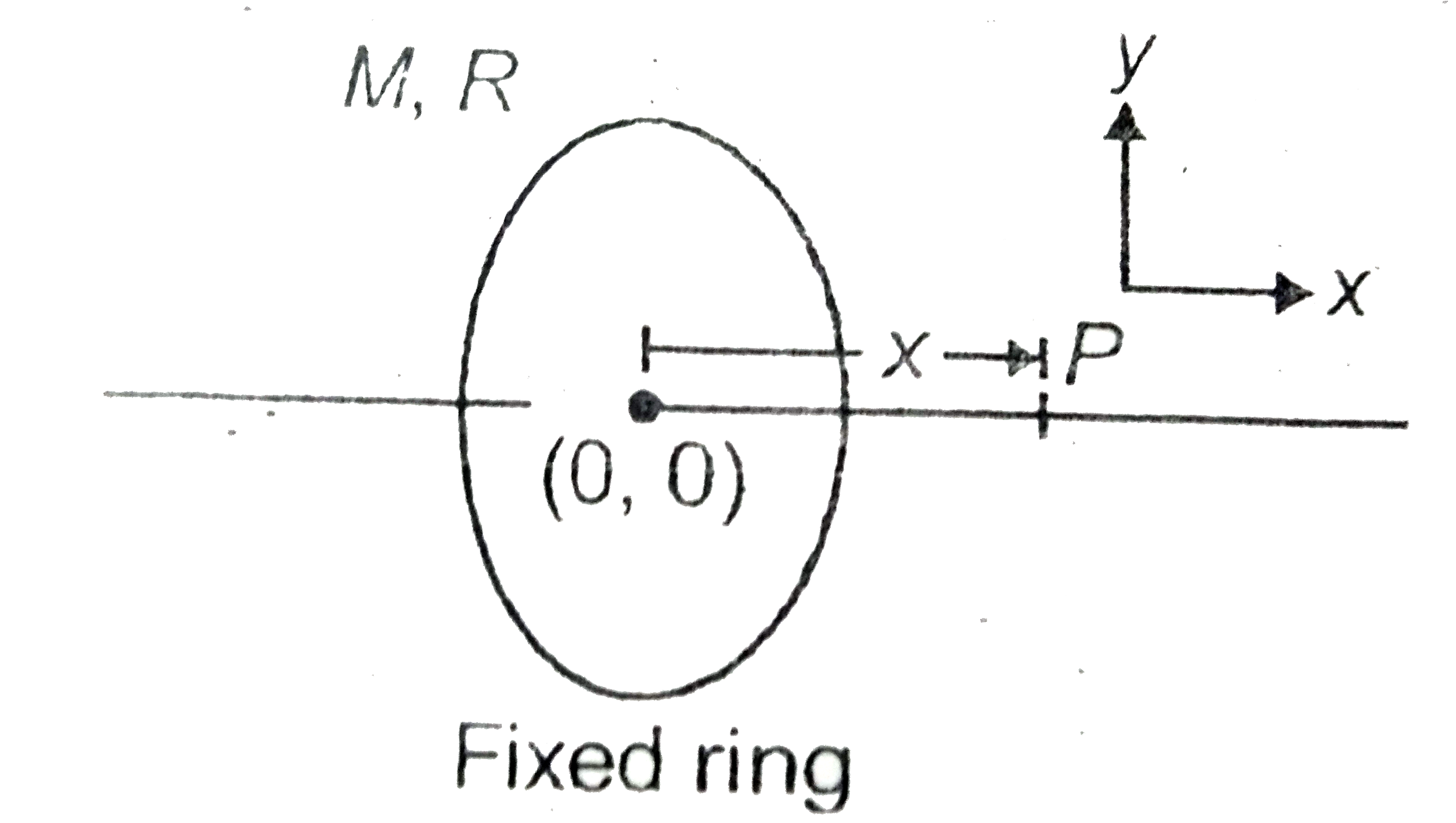
The value of maximum gravitational field intensity is
View Solution
Knowledge Check
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRA point mass m0 is placed at distance R/3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m0 is
A4Gmm0R2BzeroC9Gmm0R2DNone of theseConsider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
AGmr2B2Gm√3r2C2Gm3√3r2DGm2r2
The gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
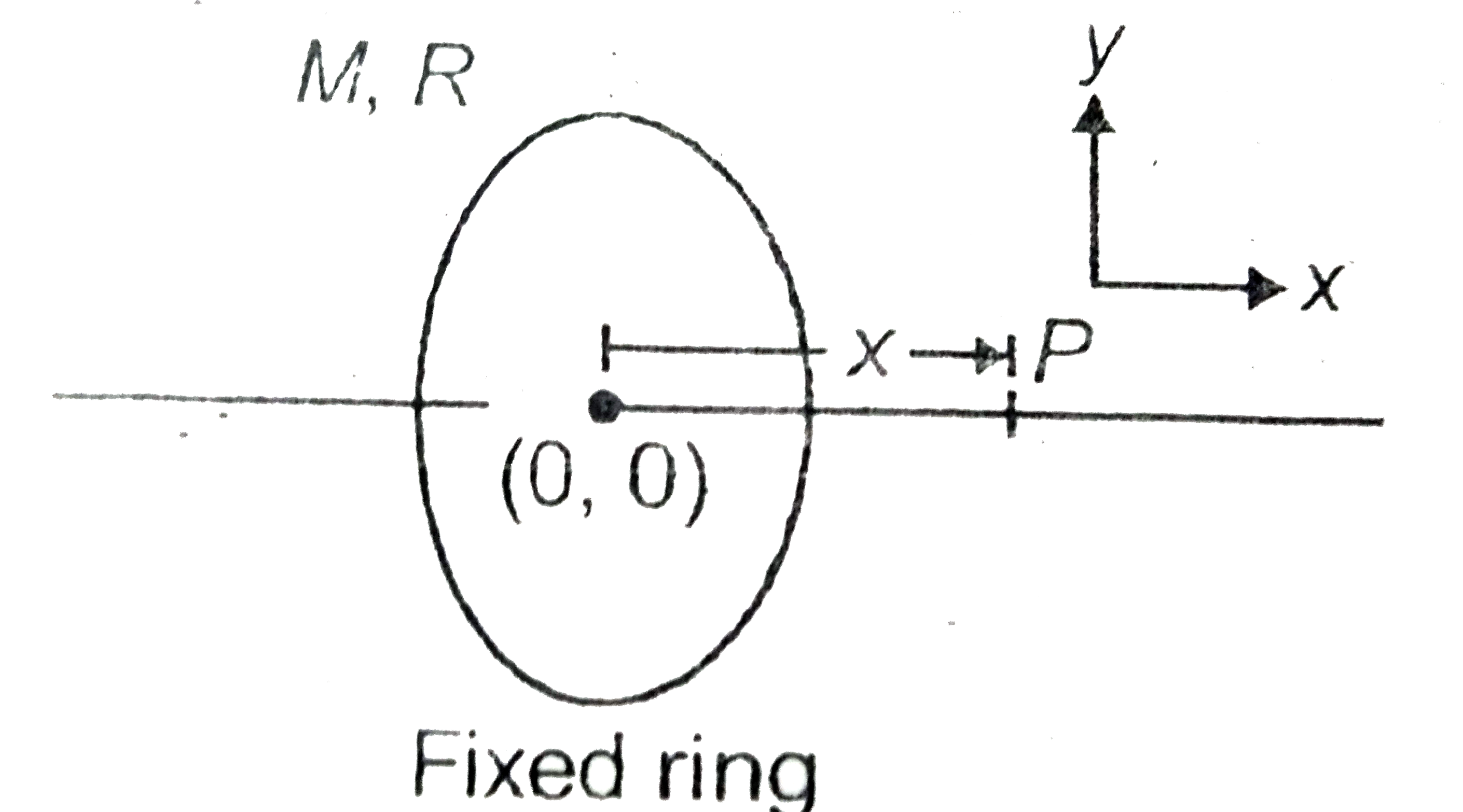
The intensity of gravitational field has the maximum value at x equal to
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
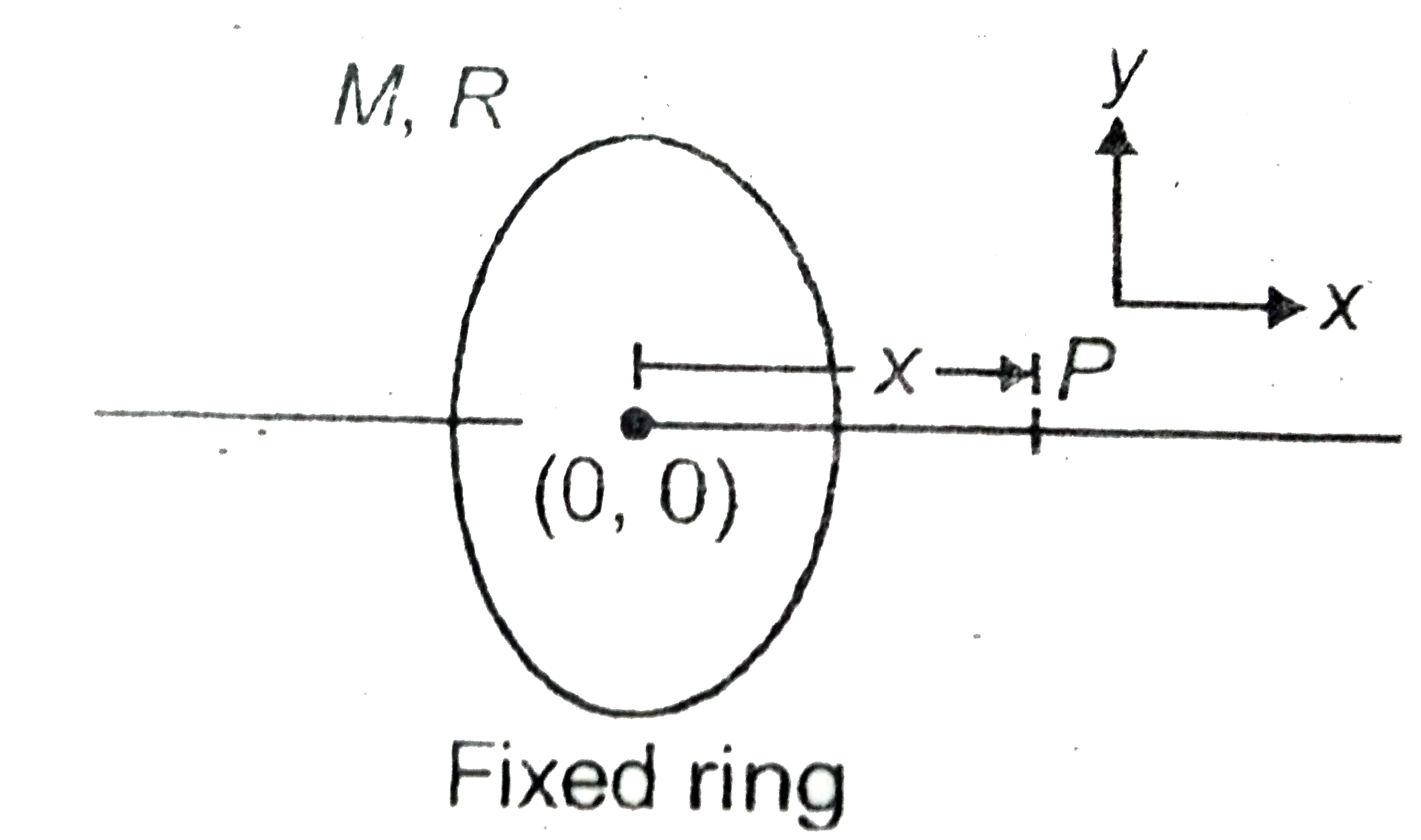
For a point near to the centre i.e., x lt lt R, the intensity of gravitational field E
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
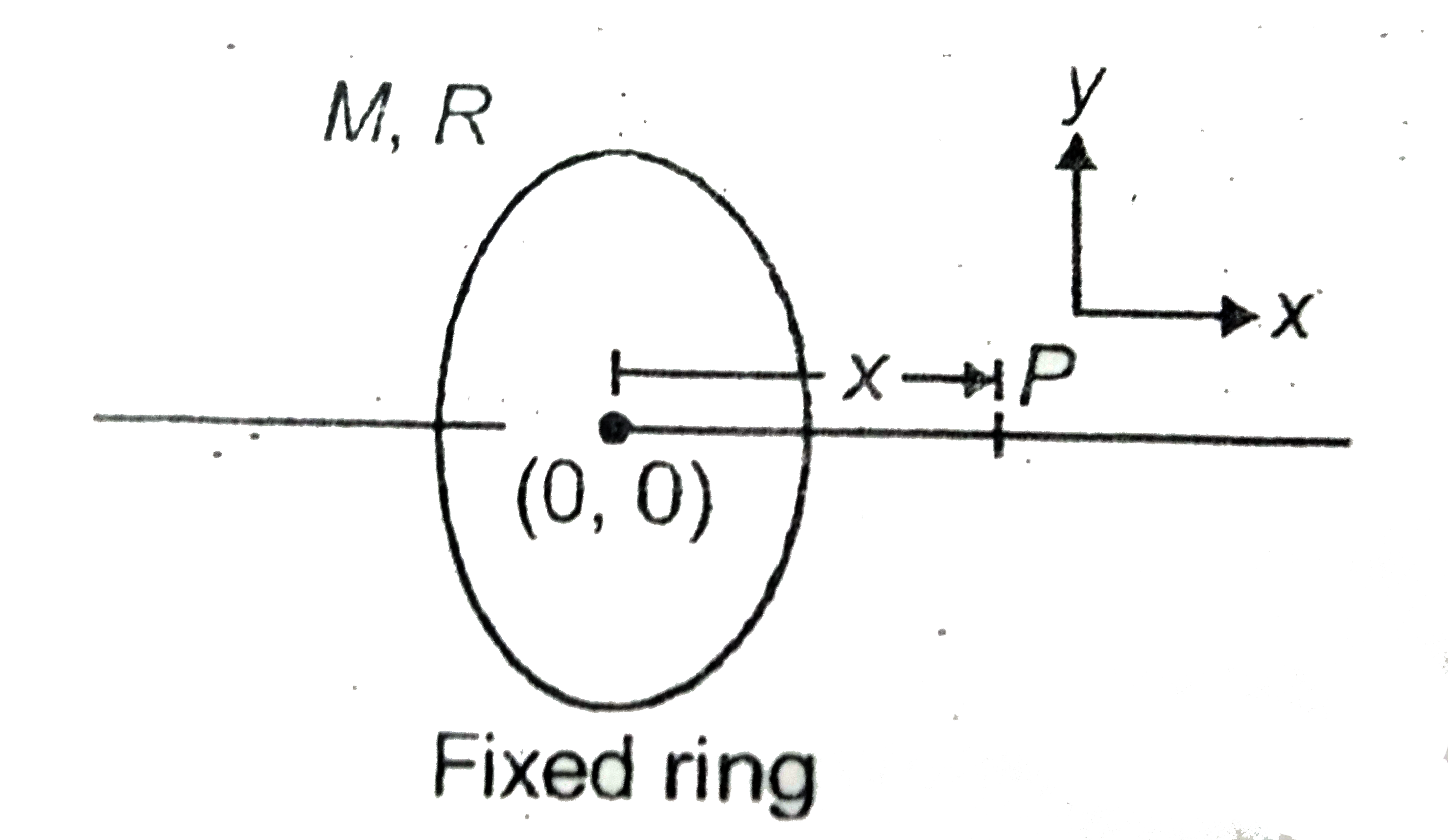
If the particle (mass m) is released from rest from a point distant x=R√3, then it will pass through the centre of ring with speed
View SolutionFind the potential V at P in the gravitational field of fixed point mass M.
View SolutionA mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass M is
View Solution
