For Question , calculat the block's speed asit passes through the equilibrium point ?
Hint :E=K+U=12mv2+12kx2=12mv2+0 . Calculate v
We want the speed at x=0 where the PE is U=12kx2=0 and the mechanical energy is entirely kinetic energy ,
So, E=K+U=12mv2+12kx2+=12mv2+0
8.588×107=12×(5.44×105kg)v2
v=17.77m/s
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)58videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )25videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)13videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)5videos
PHYSICAL WORLD
Similar Questions
For example , at what displacement the kinetic is eqal to the potential energy ?
Hint :U=12kx2,K=12(A2−x2)
U=KView SolutionAn electron of mass m is involved in head-on collision with an atom of mass M , initially at rest . As a result of the collision a certain amount of energy E is stored internally in the atom . What is the minimum initial velocity that the electron must have ?
[Hint : Since energy is stored in the atom , the collision is essentially inelastic . mv = mv' + Mv'' and 12mv2=E+12mv2+12Mv''2 . Solve for v' and apply the condition for real values of v'.)View Solution
Knowledge Check
- Question 1 - Select One
The equation of the plane that passes through the points (1,0,2),(1,1,2),(5,0,3) is
Ax+2y-4z+7=0Bx+2y-3z+7=0Cx-2y+4z+7=0D2y-4z-7+x=0
Check the dimensional consistency of the relations :
(i) S=ut+12at2
(ii) 12mv2=mgh.View SolutionPassing through the points (−1,1), and (2,−4).
View SolutionFor examples 15, find the potential energy of the block at 0.05 m from the mean position
Hint :P.E.=12kx2View Solution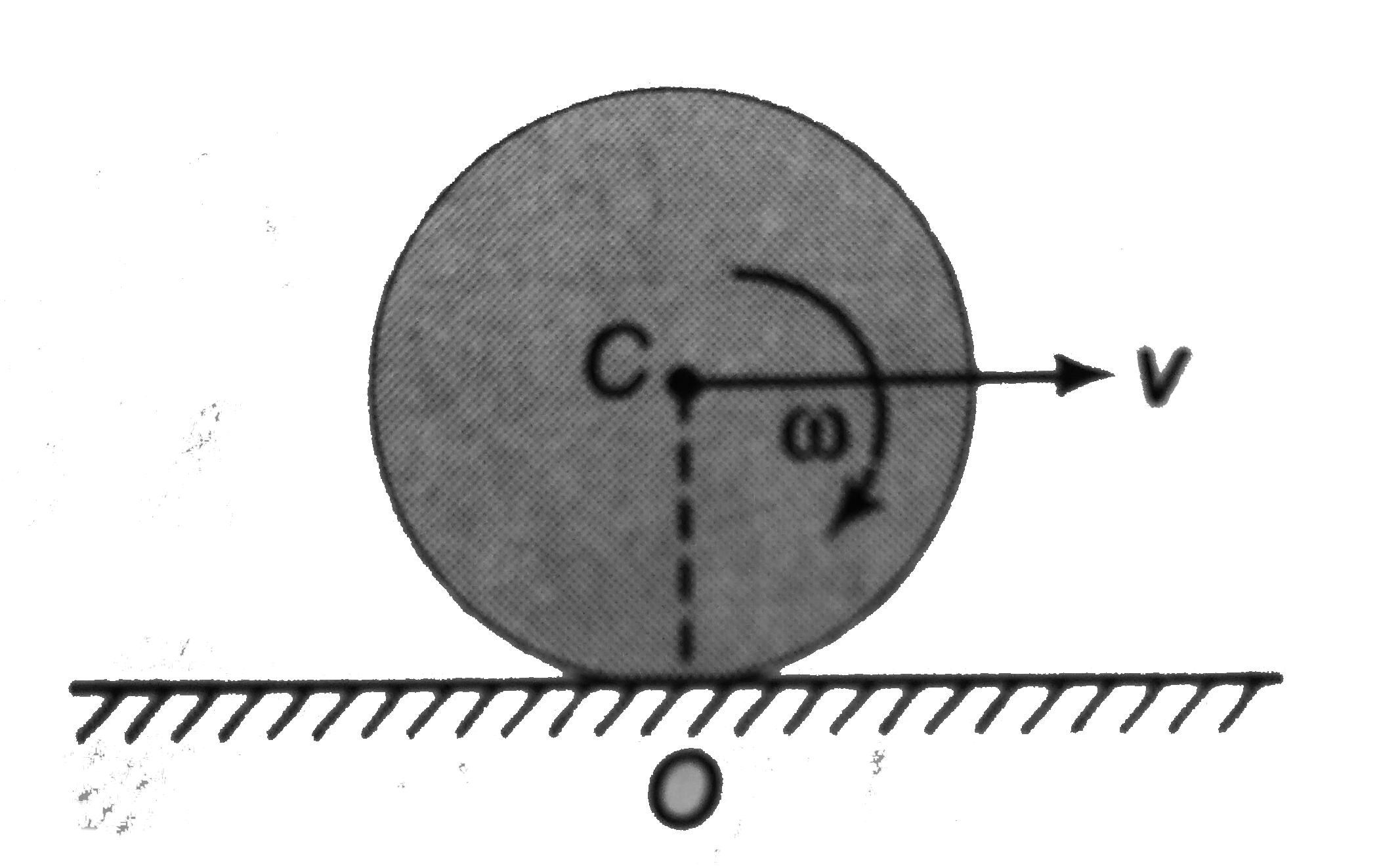
A solid sphere is rolling without slipping as shown in figure. Prove that
12mv2+12lCω2=12l0ω2View SolutionWrite the logarithmic equation for E=12mv2
View SolutionFind the equations of the plane that passes through three points (1,1,0),(1,2,1),(-2,2,-1).
View SolutionDirection ratios of the normal to the plane passing through the point (0,1,1),(1,1,2)and(−1,2,−2) are
View Solution

