Find the relatio between volume and temperature of a gas in a process, in which the molar heat capacity C varies with temperature T as C=CV+αT. [α is a constant] .
By first law of thermodymanics, molar specific heat is given as
C=CV+R(dV/VdT/T) . . . . (i)
Compare (i) with given equation
C+CV+αT=CV+R(dV/VdT/T)
⇒R(dV/V)=αT(dTT)
⇒dVV=αdTR
⇒log V=αTR+logC
⇒logV=logeeαTR+logC
⇒log V=log[C.eαT/R]
⇒Ve−αT/R=C.
Similar Questions
Knowledge Check
For an ideal gas the equation of a process for which the heat capacity of the gas varies with temperatue as C=(α/T(α) is a constant) is given by
AVlnT=constantBVT1/(γ−1)_(e)α/RT=constantCV1γ−1Tα/RT=constantDVγ−1T=constantTwo moles of an ideal mono-atomic gas undergoes a thermodynamic process in which the molar heat capacity 'C' of the gas depends on absolute temperature as C=RTT0, where R is gas consant and T0 is the initial temperature of the gas. (V0 is the initial of the gas). Then answer the following questions:
The equation of process isA1P=V0T3/204RT52e(T−T0T0)B1P=V0T3/202RT52e(T−T0T0)C1P=V0T3/204RT52e(T+T0T0)D1P=V0T3/203RT52e(T−T0T0)The molar heat capacity for a gas at constant T and P is
A3/2 RB5/2 RCdepends on atomicity of gasDinfinity (∞)
What is the most likely value for CT (molar heat capacity at constant temperature) ?
View SolutionOxygen gas is made to undergo a process in which its molar heat capacity C depends on its absolute temperature T as C=αT. Work done by it when heated from an initial temperature T0 to a final temperature 2T0, will be
View SolutionFigure shows a process on a gas in which pressure and volume both change. The molar heat capacity for this process is C.
View SolutionThe pressure P of an ideal diatomic gas varies with its absolute temperature T as shown in figure. The molar heat capacity of gas during this process is [R is gas constant]
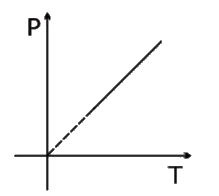
View SolutionAn ideal gas undergoes a process in which co-efficient of volume expansion of gas γ, varies with absolute temperature by the relation γ=2T. Let C is molar heat capacity in this process and Cp.CV are molar heat capacities at constant pressure and volume respectively. Then
View Solution
