Question

If the slope for isotherm is X and the slope for adiabat is Y then

Options

A. X=`gammaY`
B. `Y=gammaX`
C. X=Y
D. `X^(gamma)=Y`

Answer

B

Explanation

To solve the problem regarding the slopes of isotherms and adiabats in thermodynamics, we will derive the relationship between the slopes $$X$$ (for isotherm) and $$Y$$ (for adiabat).

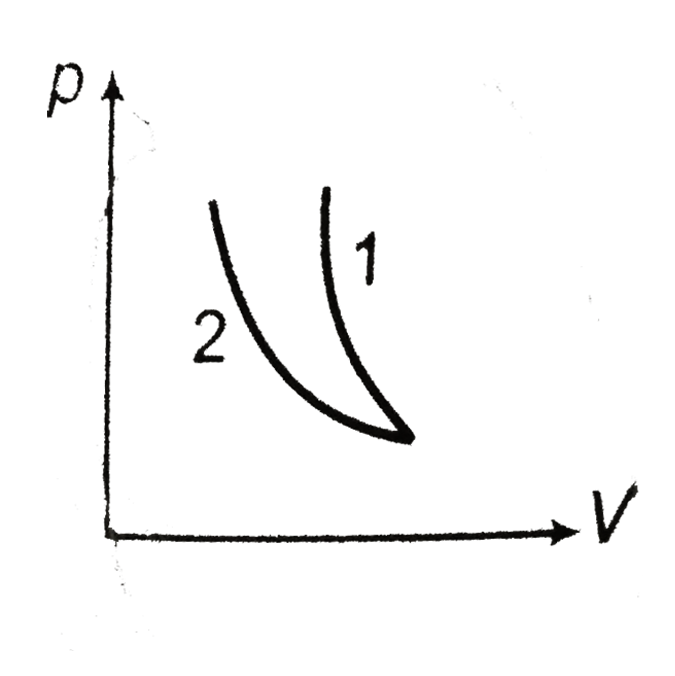
1. Understanding Isotherm and Adiabat:
- An isotherm is a curve on a pressure-volume (P-V) diagram where the temperature remains constant.
- An adiabat is a curve on a P-V diagram where no heat is exchanged with the surroundings.

2. Differentiating the Isotherm Equation:
- For an isothermal process, we can use the ideal gas law:
\( PV = nRT \)
- Differentiating this with respect to volume \(V\) gives:
\( PdV + VdP = 0 \)
- Rearranging this, we find:
\( \frac{dP}{dV} = -\frac{P}{V} \)
- The slope of the isotherm, denoted as \(X\), can be represented as:
\( X = -\frac{P}{V} \)

3. Differentiating the Adiabat Equation:
- For an adiabatic process, the relationship can be expressed as:
\( PV^\gamma = \text{constant} \)
- Differentiating this gives:
\( PdV + VdP \cdot \gamma = 0 \)
- Rearranging this, we find:
\( \frac{dP}{dV} = -\frac{\gamma P}{V} \)
- The slope of the adiabat, denoted as \(Y\), can be represented as:
\( Y = -\frac{\gamma P}{V} \)

4. Relating the Slopes \(X\) and \(Y\):
- Now, we can relate the slopes \(X\) and \(Y\):
\( \frac{X}{Y} = \frac{-\frac{P}{V}}{-\frac{\gamma P}{V}} = \frac{1}{\gamma} \)
- This implies:
\( \gamma X = Y \)

5. Conclusion:
- The relationship between the slopes of the isotherm and the adiabat is given by:
\( Y = \gamma X \)