The variation of pressure versus volume is shown in the figure. The gas is diatomic and the molar specific heat capacity for the process is found to xR. Find the value of x.
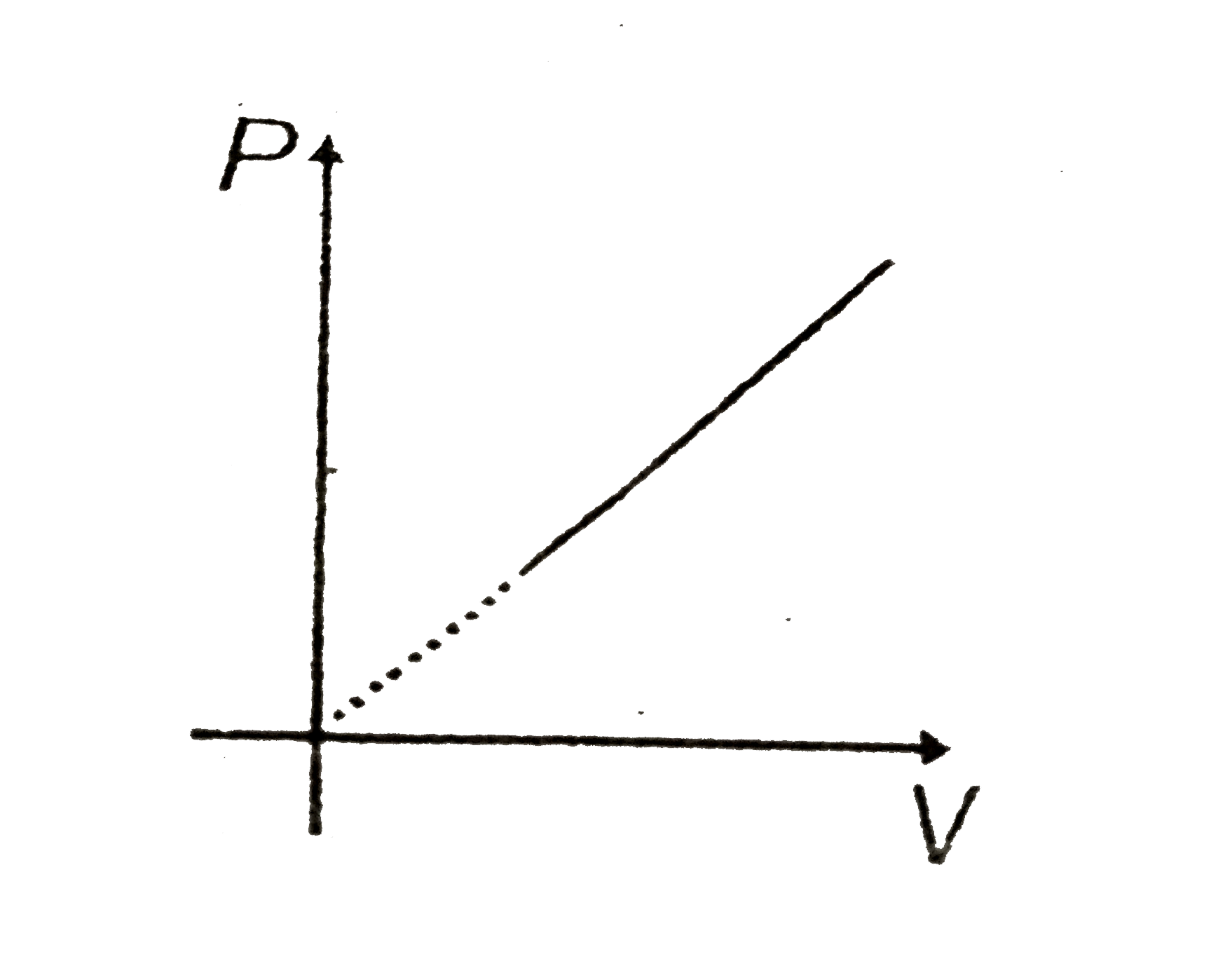 .
.
The correct Answer is:3
Step by step video & image solution for The variation of pressure versus volume is shown in the figure. The gas is diatomic and the molar specific heat capacity for the process is found to xR. Find the value of x. . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTECHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-H) Multiple True-False Type Question
2 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTECHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-I) Subjective Type
5 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTECHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-F) Matrix-Match type Question
5 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTECHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-J) Akash Challengers Questions
7 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTECHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
Knowledge Check
Molar specific heat capacity of nitrogen gas is
Aless than that of hydrogen gasBgreater than that of hydrogen gasCsame as that of hydrogen gas,DNone of these.The molar heat capacity for the process shown in figure is
 AC=CpBC=CvCC>CvDC=0
AC=CpBC=CvCC>CvDC=0The molar heat capacity for the process shown in fig. is
 AC=CvBC=CpCC>CvDC<Cv
AC=CvBC=CpCC>CvDC<Cv
The molar heat capacity for the process shown in fig. is
View SolutionThe molar heat capacity of a gas in a process
View SolutionAt constant volume, for different diatomic gases, the molar specific heat
View SolutionIf molar heat capacity of the given process (as shown in figure) is C, then

View SolutionThe variation of pressure P with volume V for an ideal diatomic gas is parabolic as shown in the figure. The molar specific heat of the gas during this process is

View Solution
