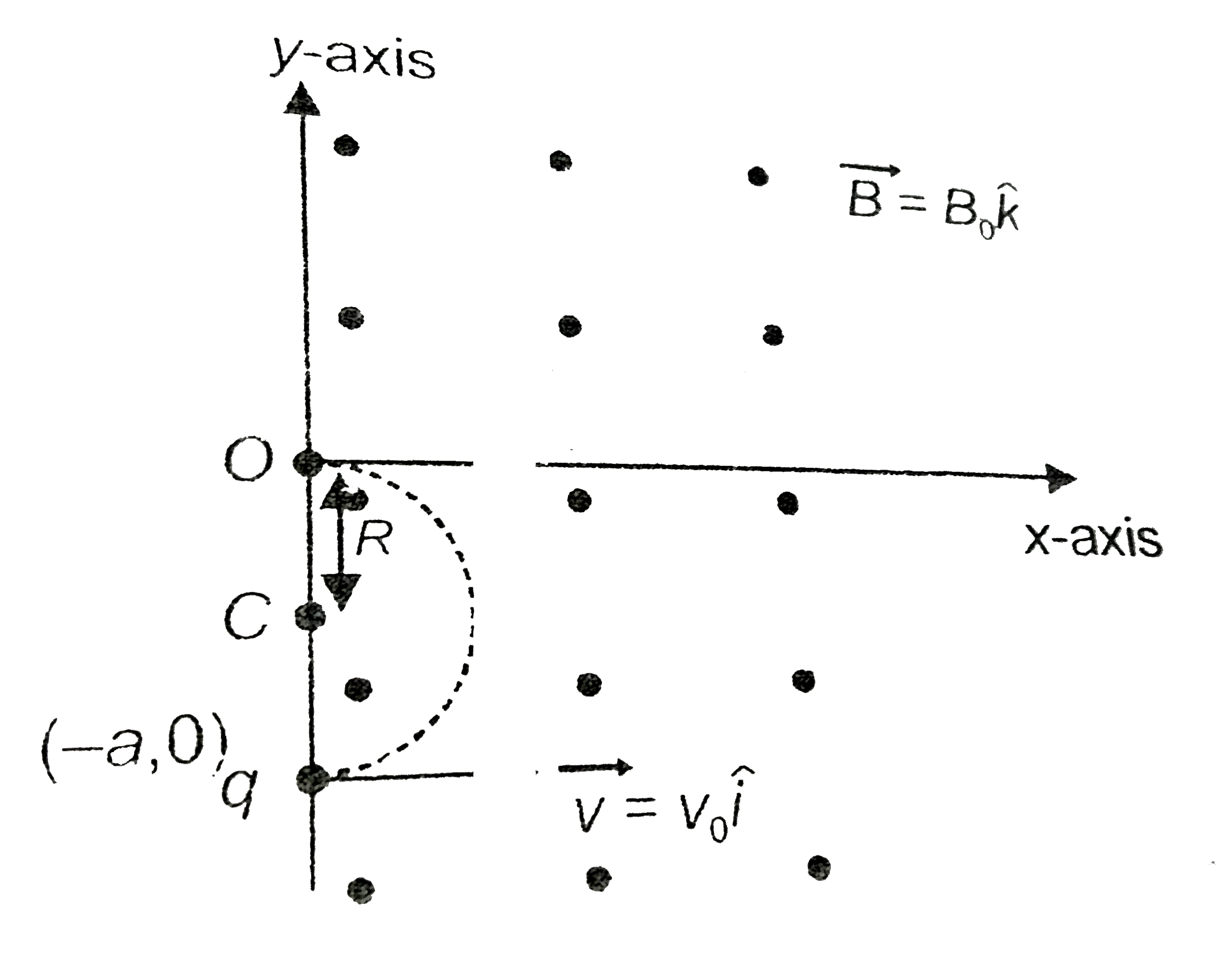
There exists a uniform magnetic field →B=+B0ˆk for x>0and→B=0 for all x<0. A charged particle placed at (0,−a,0) is given an initial velocity →v=v0ˆi. What is the magnitude and nature of charge on the particle such that it crosses through the origin ?
Strategy: When the charge is projected perpendicular to a uniform magnetic field, it follows a circular path. In this case, the force acting on it will be directed either towards +y-axis. or y-axis. It is given that it crosses point O. Thus, the force at (0,−a,0) must be towards y-axis
→F=q(→v×→B)
⇒→F=q(v0ˆi×B0ˆk)=−qv0Bˆj
⇒ q must be negative
Let C be the centre of the circle
such that R=a2
mv0|q|B0=a2
∴q=−2mv0B0a
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration12videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself27videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D16videos
MOVING CHARGE AND MAGNESIUM
- BOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
Similar Questions
Electric field and magnetic field in a region of space are given by(Ē=E0ˆj). and (¯¯¯B=B0ˆj). A charge particle is released at origin with velocity (¯v=v0ˆk) then path of particle is
View SolutionWhat is the direction of the force acting on a charged particle q, moving with a velocity →v a uniform magnetic field →B ?
View Solution
Knowledge Check
- Question 1 - Select One
Assertion In a uniform magnetic field B=B0ˆk, if velocity of a charged particle is v0ˆi at t = 0, then it can have the velocity v0ˆj at some other instant.
Reason In uniform magnetic field, acceleration of a charged particle is always zero.AIf both Assertion and Reason are true and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are true but Reason is not correct explanation of Assertion.CIf Assertion is true but Reason is false.DIf Assertion is false but Reason is true. - Question 2 - Select One
A charged particle moves with velocity →v=aˆi+dˆj in a magnetic field →B=Aˆi+Dˆj. The force acting on the particle has magnitude F. Then,
AF=0,ifaD=dA.BF=0,ifaD=−dA.CF=0,ifaA=−dD.Df∝(a2+b2)1/2×(A2+D2)1/2 - Question 3 - Select One
There exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is
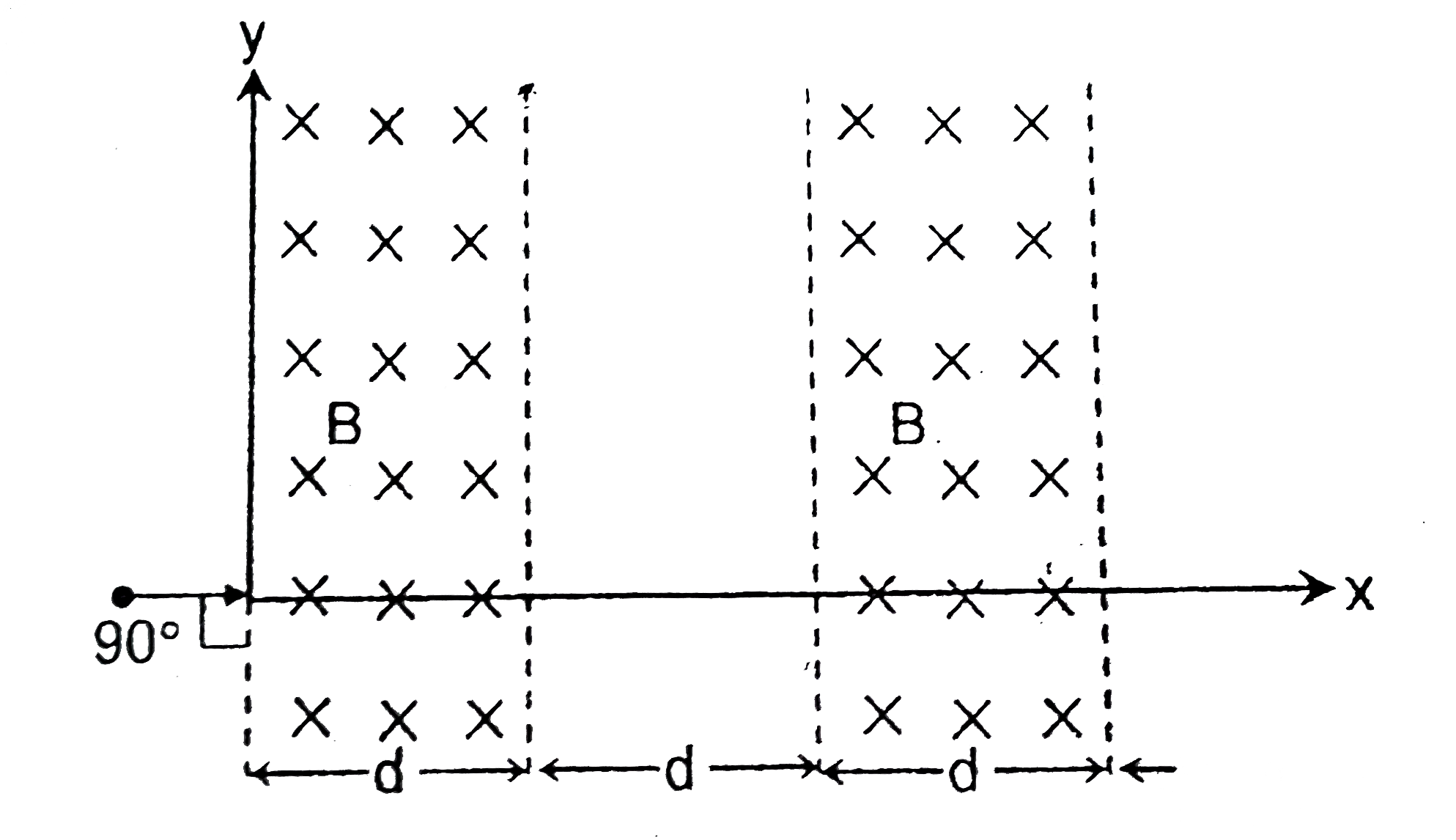 Am2qBB2mqBsin−1(dR)CmqBDmqBsin−1(dR)
Am2qBB2mqBsin−1(dR)CmqBDmqBsin−1(dR)
A magnetic field →B=−B0ˆi exists within a sphere of radius R=v0T√3 where T is the time period of one revolution of a charged particle starting its motion form origin and moving with a velocity vce(v)0=v02√3ˆi−v02ˆj. Find the number of turns that the particle will take to come out of the magnetic field.
View SolutionThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is
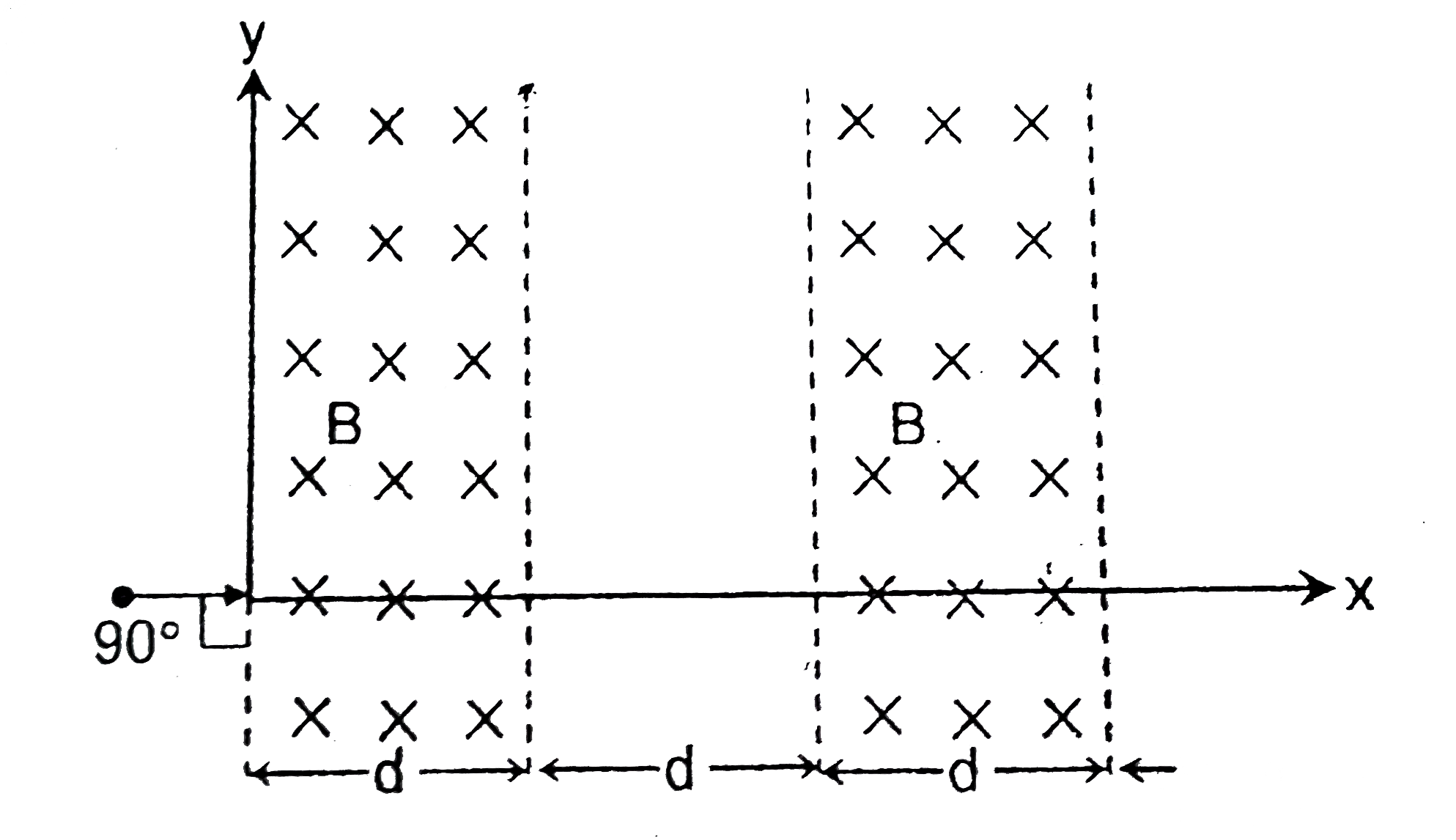 View Solution
View SolutionA magnetic field →B=B0ˆj , exists in the region a<x<2a , and vec(B) = -B_(0) hat(j),∈theregion2a lt xlt 3a,whereB_(0)isapositiveconstant.Apositivep∮char≥mov∈gwithavelocityvec(v) = v_(0) hat (i),wherev_(0) is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like
 View Solution
View SolutionIn the space shown a non-uniform magnetic field →B=B0(1+x)(−ˆk) tesla is present. A closed loop of small resistance, placed in the xy plane is given velocity V0. The force due to magnetic field on the loop is
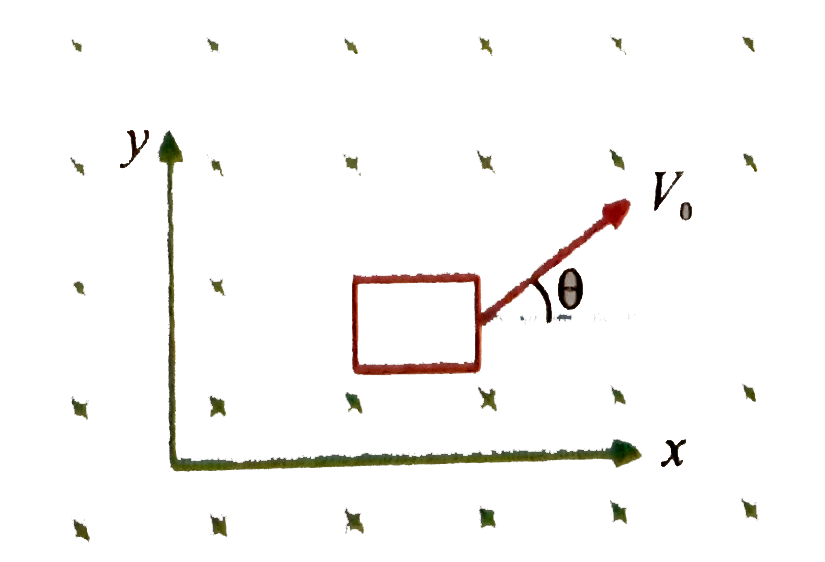 View Solution
View SolutionA magnetic field →B=B0ˆj exists in the region a<x<2a and →B=−B0ˆi in the region 2a<x<3a, where B0 is positive constant. A positive point charge moving with a velocity →v=v0ˆi where v0 is a positive constant, enters.
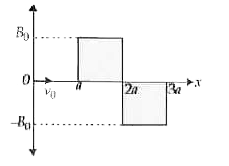
the magnetic field at x=a, The trajectory of the charge in this region can be like,View Solution

