A particle of charge q and mass m released from origin with velocity $\to v = v_{0} ˆ i$ into a region of uniform electric and magnetic fields parallel to y-axis. i.e., $\to E = E_{0} ˆ j and \to B = B_{0} ˆ j$ . Find out the position of the particle as a functions of time
Strategy : Here $\to E ∣ ∣ \to B$
The electric field accelerates the particle in y-direction i.e., component of velocity goes on increasing with acceleration
$a_{y} = \frac{F_{y}}{m} = \frac{F_{e}}{m} = \frac{q E_{0}}{m}$
The magnetic field rotates the particle in a circle in x-z plane (perpendicular to magnetic field) The resultant path of the particle is a helix with increasing pitch.
Velocity of the particle at time t would be
$\to v (t) = v_{x} ˆ i + v_{y} ˆ j + v_{z} ˆ k$

Video Solution

Text Solution

Verified by Experts

Here $v_{y} = a_{y} t = \frac{q E_{0} t}{m}$
$v_{x}^{2} + v_{z}^{2} = constant = v_{0}^{2}$
$θ = ω t = \frac{B q t}{m}$
$v_{x} = v_{0} cos θ = v_{0} cos (\frac{B q t}{m})$
$v_{z} = v_{0} sin θ = v_{0} sin (\frac{B q t}{m})$
$\to v (t) = v_{0} cos (\frac{B q t}{m}) ˆ i + (\frac{q E_{0} t}{m}) ˆ j + v_{0} sin (\frac{B q t}{m}) ˆ k$
Position vector of particle at time t can be given by
$\to r (t) = x ˆ i + y ˆ j + z ˆ k$
$y = \frac{1}{2} a_{y} t^{2} = \frac{1}{2} (\frac{q E_{0}}{m}) t^{2}$
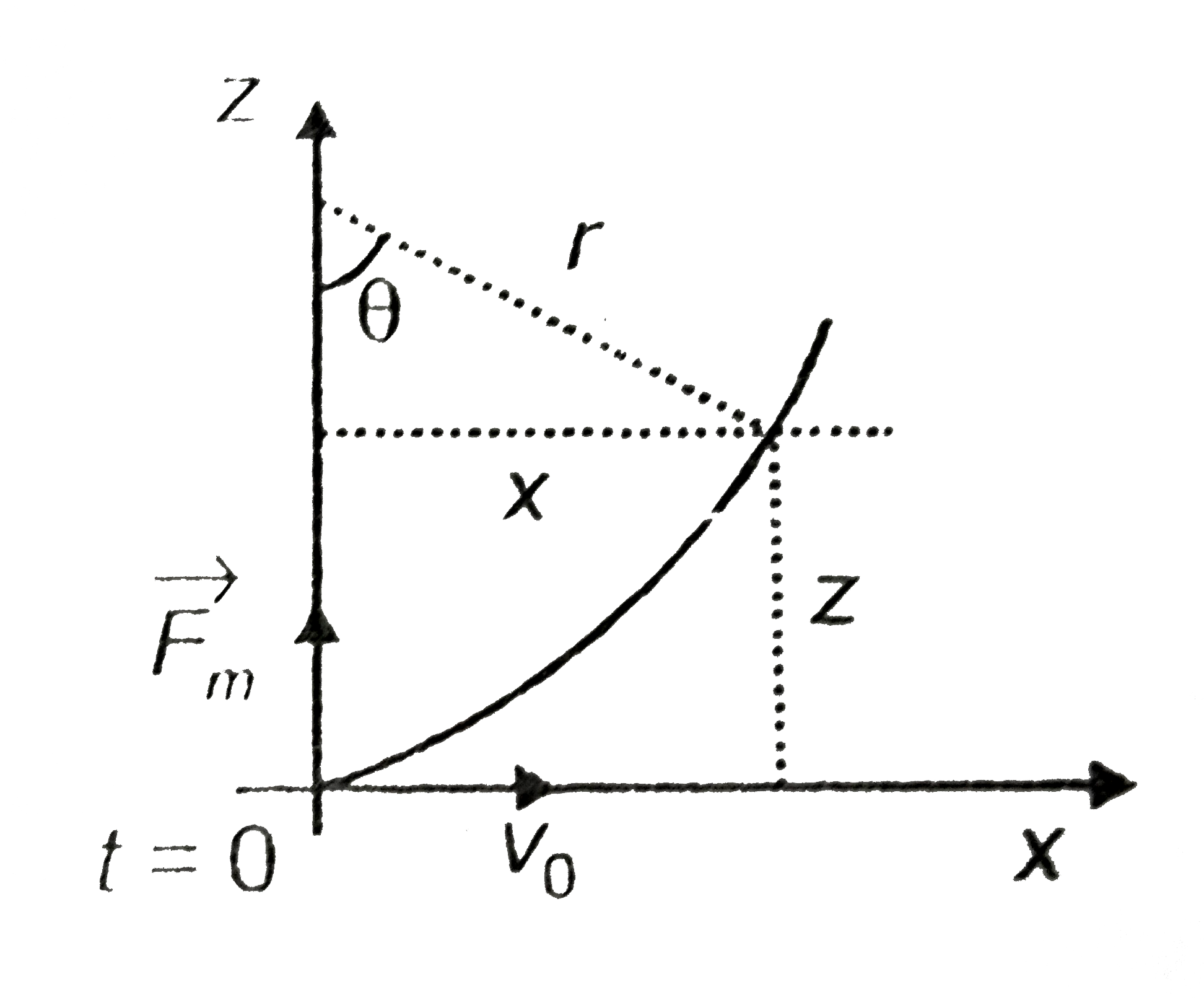
$x = r sin θ = (\frac{m v_{0}}{B q}) sin (\frac{B q t}{m})$
$z = r (1 - cos θ) = (\frac{m v_{0}}{B q}) [{1 - cos (\frac{B q t}{m})}]$
$\to r (t) = (\frac{m v_{0}}{B q}) sin (\frac{B q t}{m}) ˆ i + \frac{1}{2} (\frac{q E_{0}}{m}) t^{2} ˆ j + \frac{m v_{0}}{B q} [{1 - cos (\frac{B q t}{m})}] ˆ k$

Updated on:21/07/2023

A portion is fired from origin with velocity $\to v = v_{0} ˆ j + v_{0} ˆ k$ in a uniform magnetic field $\to B = B_{0} ˆ j$ . In the subsequent motion of the proton
Aits z co-ordinate can never be negative
Bits x co-ordinate can never be positive
Cits x and z co-oridinate cannot be zero at the same time
Dits y co-ordinate will be proportional to its time of flight
A charged particle of specific charge (charge/mass) $α$ released from origin at time $t = 0$ with velocity $\to v = v_{0} (ˆ i + ˆ j)$ in uniform magnetic field $\to B = B_{0} ˆ i .$ Coordinates of the particle at time $t = π / (B_{0} α)$ are
A $(\frac{v_{0}}{2 B_{0} α}, \frac{\sqrt{2} v_{0}}{α B_{0}}, \frac{- v_{0}}{B_{0} α})$
B $(\frac{v_{0}}{2 B_{0} α}, 0, 0)$
C $(0, \frac{2 v_{0}}{B_{0} α}, \frac{v_{0} π}{2 B_{0} α})$
D $(\frac{v_{0} π}{B_{0} α}, 0, \frac{- 2 v_{0}}{B_{0} α})$
If $\to A = 3 ˆ i - 4 ˆ j$ and $\to B = 2 ˆ i + 16 ˆ j$ then the magnitude and direction of $\to A + \to B$ will be
A $5, {tan}^{- 1} (12 / 5)$
B $10, {tan}^{- 1} (5 / 12)$
C $13, {tan}^{- 1} (12 / 5)$
D $12, {tan}^{- 1} (5 / 12)$