A fish is a little away below the surface of a lake. If the critical angle is 49∘ , then the fish could see things above the water surface withing an angular range of θ∘ where

θ=49∘
θ=90∘
θ=98∘
θ=24.5∘
The correct Answer is:C
Step by step video, text & image solution for A fish is a little away below the surface of a lake. If the critical angle is 49^(@) , then the fish could see things above the water surface withing an angular range of theta^(@) where by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - B) Objective Type Questions (One option is correct)16videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - AAKASH INSTITUTECHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)10videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - AAKASH INSTITUTECHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - D)16videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)5videos
PHYSICAL WORLD
- BOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)10videos
SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )
Similar Questions
At what angle with the water surface does fish in figure see the setting sun ?
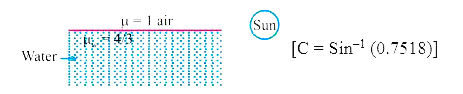 View Solution
View SolutionA small fish 0.4 m below the surface of a lake is viewed through a simple converging lens of focal length 3 m.the lens is kep at 0.2 m above the water surface such that the fish lies on the optical axis of the lens. Find the image of the fish seen by the observed. (μwater=43)
View Solution
Knowledge Check
- Question 1 - Select One
The length of a vertical pole at the surface of a lake of water (μ=43) is 24 cm. Then to an under-water fish just below the water surface the tip of the pole appeard to be
A18 cm above the surfaceB24 cm above the surfaceC32 cm above the surfaceD36 cm above the surface - Question 2 - Select One
A man looks down on a fish of length 20 cm. His eye is 2m above the surface of the water (μ=4/3) and the fish is 2m below the surface as shown in the figure the ratio of angular width Δθ of the fish as seen by the man in presence of water to the Δθ in the absence of water is (Δθ is small)
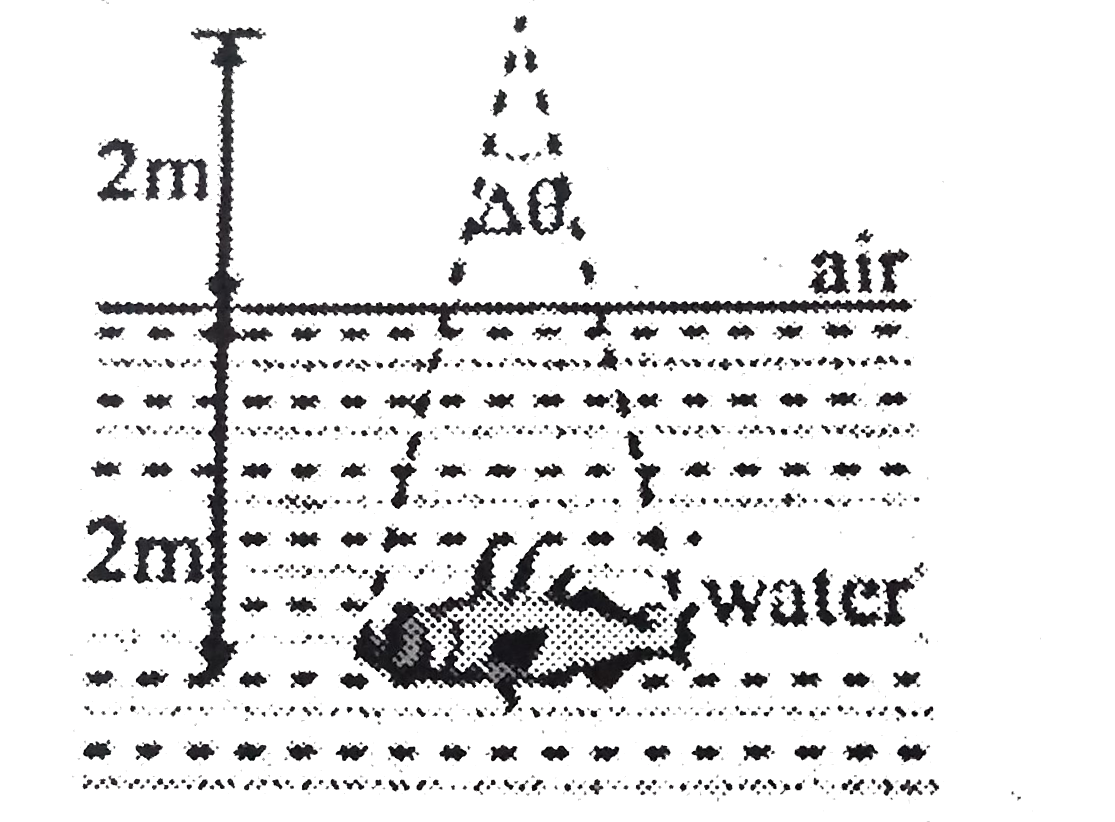 A65B5/6C7/8D8/7
A65B5/6C7/8D8/7 - Question 3 - Select One
The image of an object O due to reflection from the surface of a lake is elongated due to the ripples on the water surface caused by a light breeze. This is because the ripples act as tilted mirrors as shown. Consider the case where O and the observer E are at the same height above the surface of the lake. If the maximum angle that the ripples make with the horizontal is a, the angular extent δ of the image will be
 Aα2BαC2αD4α
Aα2BαC2αD4α
A small fish 0.4m below the surface of a lake, is viewed through a simple converging lens of focal length 3m. The lens is kept at 0.2m above the water surface such that the fish lies on the optical axis of the lens. Find the distance of the image of the fish from the lens as seen by the observer. The refractive index of water is 4/3.
View SolutionUnpolarized red light is incident on the surface of a lake at incident angle θR. An observer seeing the light reflected from the water surface through a polarizer notices that on rotating the polarizer, the intensity of light drops to zero at a certain orientation. The red light is replaced by unpolarized blue light. The observer sees the same effect with reflected blue light at incident angle θB. Then
View SolutionA point source of light is placed at a distance h below the surface of a large deep lake.
(a) Show that the fraction f of the light energy that escapes directly from the water surface is independent of h and is given by f=12−12n√n2−1 where n is the index of refraction of water.
(Note: Absorption within the water and reflection at the surface, except where it is total, have been neglected)
(b) Evaluate this ratio for n=4/3.View SolutionA small fish, 0.4m below the surface of a lake, is viewed through a simple converging lens of focal length 3m. The lens in kept at 0.2m above the water surface such that the fish lies on the optical axis of the lens. Find the image of the fish seen by the observer. The refractive index of water is 4/3.
View SolutionA bird is flying 3m above the surface of water. To a fish underwater, the height of the bird from the water surface appears to be
View Solution

