In the triangle ABC, lines OA,OB and OC are drawn so that angles OAB, OBC and OCA are each equal to ω, prove that cotω=cotA+cotB+cotC
Step by step video & image solution for In the triangle ABC, lines OA,OB and OC are drawn so that angles OAB, OBC and OCA are each equal to omega, prove that cotomega=cotA+cotB+cotC by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In given triangle ABC ,OB and OC are bisectors of ∠Ba nd ∠C respectively then ∠BOC is equal to
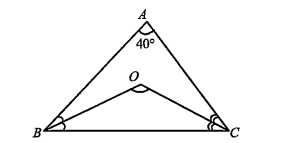 A70∘B110∘C140∘D80∘
A70∘B110∘C140∘D80∘
Angle A, B, C of a triangle ABC are equal to each other. Prove that ABC is equilateral.
View SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
OB=OC
View SolutionA B C are the points on x, y and z axes respectively in a three dimensional co-ordinate system with O as origin. Suppose the area of triangles OAB, OBC and OCA are 4, 12 and 6 respectively, then the area of the triangle ABC equals (A) 16 (B) 14 (C) 28 (D) 32
View SolutionO is the origin and lines OA, OB and OC have direction cosines lr,mrandnr(r=1,2and3). If lines OA', OB' and OC' bisect angles BOC, COA and AOB, respectively, prove that planes AOA', BOB' and COC' pass through the line xl2+l2+l3=ym1+m2+m3=zn1+n2+n3.
View SolutionO is the origin and lines OA, OB and OC have direction cosines lr,mrandnr(r=1,2and3). If lines OA', OB' and OC' bisect angles BOC, COA and AOB, respectively, prove that planes AOA', BOB' and COC' pass through the line xl1+l2+l3=ym1+m2+m3=zn1+n2+n3.
View SolutionPQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is . Then prove that the height of the tower is (abc) tanθ4.
View SolutionPQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is . Then prove that the height of the tower is (abc) tanθ4.
View Solution
