One and only one straight line can be drawn passing through two given points and we can draw only one triangle through non-collinear points. By integral coordinates (x,y) of a point we mean both x and y as integers .
The number of points in the cartesian plane with integral coordinates satisfying the inequalities |x|≤4,|y|≤4and|x−y|≤4 is

A

17

B

91

C

61

D

64

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for One and only one straight line can be drawn passing through two given points and we can draw only one triangle through non-collinear points. By integral coordinates (x,y) of a point we mean both x and y as integers . The number of points in the cartesian plane with integral coordinates satisfying the inequalities |x|le 4 , |y| le 4 and |x-y| le 4 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSPERMUTATIONS AND COMBINATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • One and only one straight line can be drawn passing through two given points and we can draw only one triangle through non-collinear points. By integral coordinates (x,y) of a point we mean both x and y as integers .
    The sides AB, BC , CA of a triangles ABC have a , b and c interior points excluding vertices on their respectively . The number of triangles that can be b constructed using these interior points are vertices i

    Aab+bc+ca2
    B∑ab(a+b−2)
    C∑ab(a+b)
    Da+b+cC3−(aC3+bC3+cC3)

  • The solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is

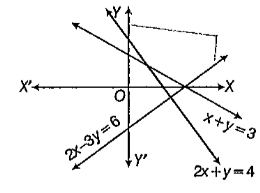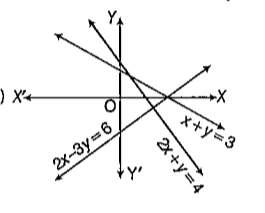    Aocr_image
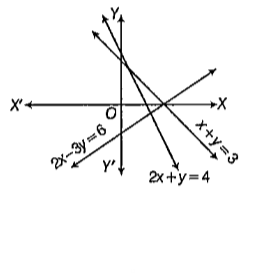    Bocr_image
    Cocr_image
    Docr_image

  • The total number of integral points i.e. points having integral coordinates lying in the region represented by the inequations |x−y|<3 and |x+y|<3 is

    A25
    B36
    C13
    D12