The symbols +,+,×,×,⋆,⋅ are placed in the squares of the adjoining figure. The number of ways of placing symbols so that no row remains empty is
16580
14580
5400
4860
The correct Answer is:B
To solve the problem of placing the symbols +,+,×,×,<strong>⋅,⋅ in such a way that no row remains empty, we can follow these steps:
Step 1: Identify the Symbols and Rows
We have the following symbols:
- 2 + symbols
- 2 × symbols
- 3 ⋅ symbols
- 1 ⋅ symbol
We need to place these symbols in 5 rows, ensuring that no row is empty.
Step 2: Choose Symbols for Each Row
Since we have 5 rows and we need to ensure that each row has at least one symbol, we can start by placing one symbol in each of the 5 rows.
Step 3: Assign Symbols to Rows
We can choose 5 symbols from the available symbols to fill the rows. The choices can be made as follows:
- Choose 1 symbol from the + symbols (2 choices)
- Choose 1 symbol from the × symbols (2 choices)
- Choose 1 symbol from the ⋅ symbols (3 choices)
- Choose 1 symbol from the ⋅ symbol (1 choice)
This gives us:
- 2 choices for +
- 2 choices for ×
- 3 choices for ⋅
- 1 choice for ⋅
Thus, the total number of ways to choose one symbol for each row is:
\( 2 \times 2 \times 3 \times 1 = 12 \)
Step 4: Choose the Remaining Symbols
After placing one symbol in each of the 5 rows, we have 6 symbols left (3 ⋅ and 2 × and 1 ⋅). We need to choose one of these symbols to fill one more row.
The number of ways to choose one symbol from the remaining 6 symbols is:
\( \binom{6}{1} = 6 \)
Step 5: Calculate Total Arrangements
Now we need to calculate the total arrangements of the symbols. The total number of arrangements of the symbols is given by:
\( \frac{6!}{2! \times 2! \times 3!} \)
Where:
- \(6!\) is the factorial of the total number of symbols.
- \(2!\) accounts for the identical + symbols.
- \(2!\) accounts for the identical × symbols.
- \(3!\) accounts for the identical ⋅ symbols.
Calculating this gives:
\( \frac{720}{2 \times 2 \times 6} = \frac{720}{24} = 30 \)
Step 6: Combine Choices and Arrangements
Finally, we multiply the number of ways to choose the symbols by the number of arrangements:
\( 12 \times 30 = 360 \)
Final Answer
The total number of ways to place the symbols in the squares so that no row remains empty is 360.
---
We have the following symbols:
- 2 + symbols
- 2 × symbols
- 3 ⋅ symbols
- 1 ⋅ symbol
Since we have 5 rows and we need to ensure that each row has at least one symbol, we can start by placing one symbol in each of the 5 rows.
We can choose 5 symbols from the available symbols to fill the rows. The choices can be made as follows:
- Choose 1 symbol from the + symbols (2 choices)
- Choose 1 symbol from the × symbols (2 choices)
- Choose 1 symbol from the ⋅ symbols (3 choices)
- Choose 1 symbol from the ⋅ symbol (1 choice)
- 2 choices for +
- 2 choices for ×
- 3 choices for ⋅
- 1 choice for ⋅
\( 2 \times 2 \times 3 \times 1 = 12 \)
After placing one symbol in each of the 5 rows, we have 6 symbols left (3 ⋅ and 2 × and 1 ⋅). We need to choose one of these symbols to fill one more row.
\( \binom{6}{1} = 6 \)
Now we need to calculate the total arrangements of the symbols. The total number of arrangements of the symbols is given by:
\( \frac{6!}{2! \times 2! \times 3!} \)
- \(6!\) is the factorial of the total number of symbols.
- \(2!\) accounts for the identical + symbols.
- \(2!\) accounts for the identical × symbols.
- \(3!\) accounts for the identical ⋅ symbols.
\( \frac{720}{2 \times 2 \times 6} = \frac{720}{24} = 30 \)
Finally, we multiply the number of ways to choose the symbols by the number of arrangements:
\( 12 \times 30 = 360 \)
The total number of ways to place the symbols in the squares so that no row remains empty is 360.
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section-I (Subjective Type Questions)
10 Videos
- MATRICESBOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Assignment (Section - J) Aakash Challengers Questions
3 Videos
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTECHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)
12 Videos
Similar Questions
The symbols ϕ,ϕ, *, *, i,Δ are placed in squares of the adjoining figures. The number of ways of placing symbols so that no row remains empty is
View SolutionIn how many ways the letters of the word DIPESH can be placed in the squares of the adjoining figure so that no row remains empty?
View Solution
Knowledge Check
The number at the place of * in the adjoining figure
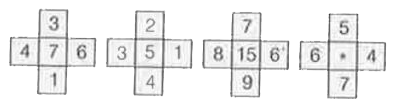
will beA10B8C9D11
In how many ways the letters of the word DIPESH can be placed in the squares of the adjoining figure so that no row remains empty?

View SolutionThe number of ways that the letters of the word ''PERSON'' can be placed in the squares of the adjoining figure so that no row remains empty
View SolutionThe number of ways the letters of the word PERSON cann be placed in the squares of the figure shown so that no row remain empty is

View SolutionThe number of rectangles in the adjoining figure is 5×5
View SolutionNumber of ways to place 10 identical balls in 3 different boxes such that no box remains empty is
View SolutionThe number of ways in which 5 X's can be placed in the squares of the figure so that no row remains empty is:
View SolutionThe number of ways in which the letters of the word PERSON can placed in the squares of the given figure so that no row remains empty is a. 24×6! b. 26×6! c. 26×7! d. 27×6!
View Solution
