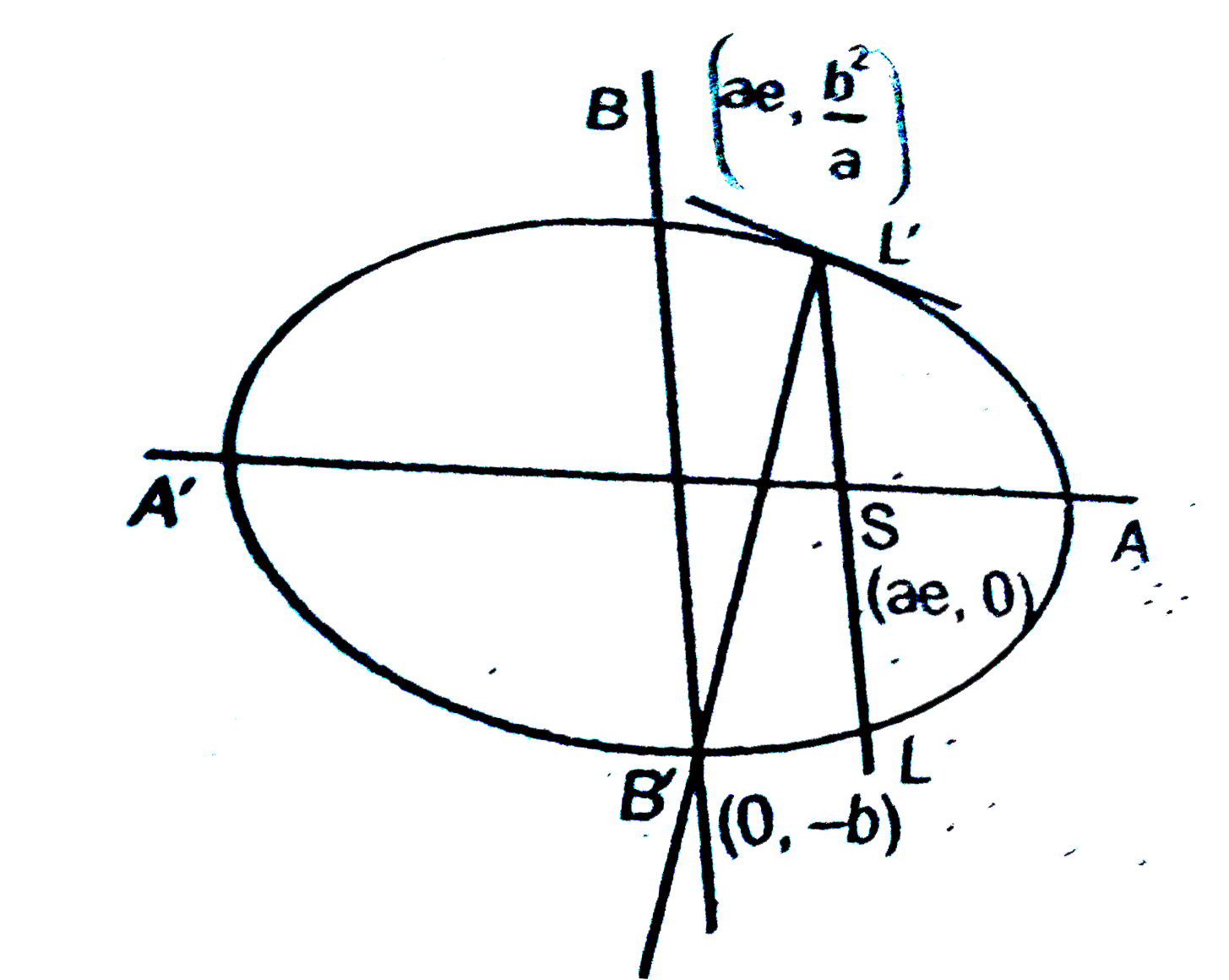
If the normals at an end of a latus rectum of an ellipse passes through the other end of the minor axis, then prove that $e^{4} + e^{2} = 1 .$

Video Solution

Text Solution

Verified by Experts

The equation of the minor of an end $L (a e, \frac{b^{2}}{a})$ of a latus rectum of the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ is given by
$\frac{x - a e}{\frac{a e}{a^{2}}} = \frac{y - \frac{b^{2}}{a}}{\frac{b^{2}}{a b^{2}}}$
$\Rightarrow y - \frac{b^{2}}{a} = \frac{1}{e} (x - a e)$
$\Rightarrow a y - b^{2} = \frac{a x}{e} - a^{2}$
which will pass through $B' (0, - b)$ if
$- a b - b^{2} = 0 - a^{2}$
$\Rightarrow a b = a^{2} - b^{2}$
$\Rightarrow a a \sqrt{1 - e^{2}} = a^{2} - a^{2} (1 - e^{2}) = a^{2} e^{2}$
$\Rightarrow 1 - e^{2} = e^{4}$
$\Rightarrow e^{4} + e^{2} = 1$

Updated on:21/07/2023