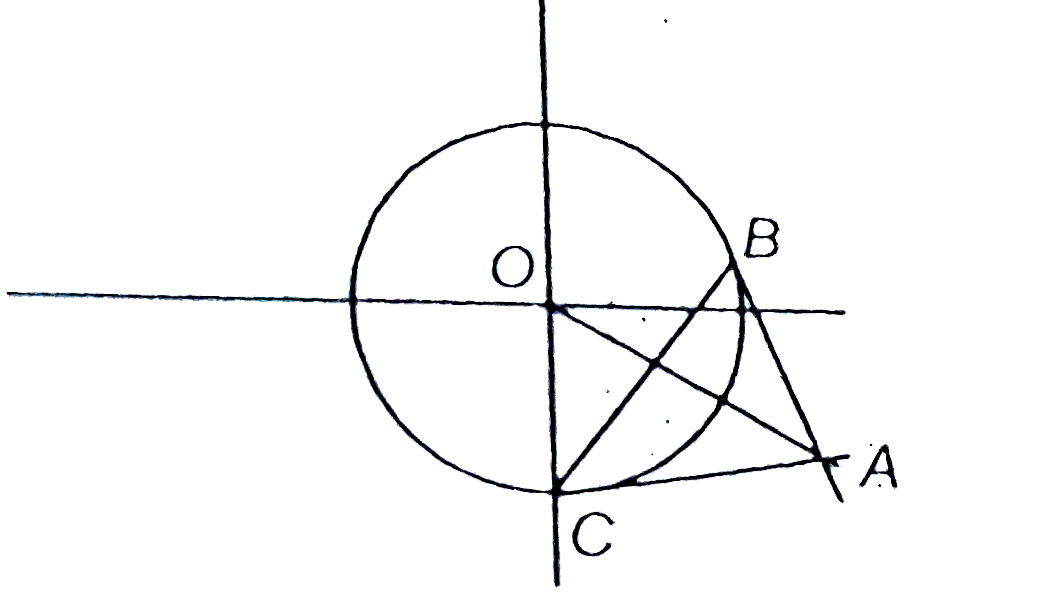
The chord of contact of tangents from 3 points A, B, C to the circle x2+y2=4 are concurrent, then the points A, B and C are.
Collinear
Topper's Solved these Questions
- CONIC SECTIONSBOOK - AAKASH INSTITUTECHAPTER - CONIC SECTIONSEXERCISE - SECTION - J ( Aakash Challengers Questions )
14 Videos
- CONIC SECTIONSBOOK - AAKASH INSTITUTECHAPTER - CONIC SECTIONSEXERCISE - SECTION - H ( Multiple True-False Type Questions )
5 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTECHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - section-J (Aakash Challengers Qestions)
16 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - AAKASH INSTITUTECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - section - J
6 Videos
Similar Questions
Statement I The chord of contact of tangent from three points A, B and C to the circle x2+y2=a2 are concurrent, then A, B and C will be collinear. Statement II A, B and C always lie on the normal to the circle x2+y2=a2.
View SolutionStatement 1 : If the chords of contact of tangents from three points A,BandC to the circle x2+y2=a2 are concurrent, then A,BandC will be collinear. Statement 2 : Lines (a1x+b1y+c1)+k(a2x+b2y+c2)=0 alwasy pass through a fixed point for k∈R .
View Solution
Knowledge Check
The chords of contact of tangents from three points A,B,C to the circle x2+y2=a2 are concurrent then the points A, B, C are
AconcyclicBcollinearCvertices of a triangleDnoneThe chord of contact of tangents from three points P, Q, R to the circle x2+y2=c2 are concurrent, then P, Q, R
Aform a triangleBare concyclicCare collinearDnone of these
Statement I The chord of contact of tangent from three points A, B and C to the circle x2+y2=a2 are concurrent, then A, B and C will be collinear. Statement II A, B and C always lie on the normal to the circle x2+y2=a2.
View SolutionThe chords of contact of tangents from three points A,BandC to the circle x2+y2=a2 are concurrent. Then A,BandC will (a)be concyclic (b) be collinear (c)form the vertices of a triangle (d)none of these
View SolutionThe chords of contact of tangents from three points A,BandC to the circle x2+y2=a2 are concurrent. Then A,BandC will (a)be concyclic (b) be collinear (c)form the vertices of a triangle (d)none of these
View SolutionThe chords of contact of tangents from three points A,BandC to the circle x2+y2=a2 are concurrent. Then A,BandC will be
View SolutionStatement 1 : If the chords of contact of tangents from three points A,B and C to the circle x2+y2=a2 are concurrent, then A,B and C will be collinear. Statement 2 : Lines (a1x+b1y+c1)+k(a2x+b2y+c2)=0 alwasy pass through a fixed point for k∈R .
View SolutionLet the midpoint of the chord of contact of tangents drawn from A to the circle x2+y2=4 be M(1,−1) and the points of contact be B and C
View Solution
