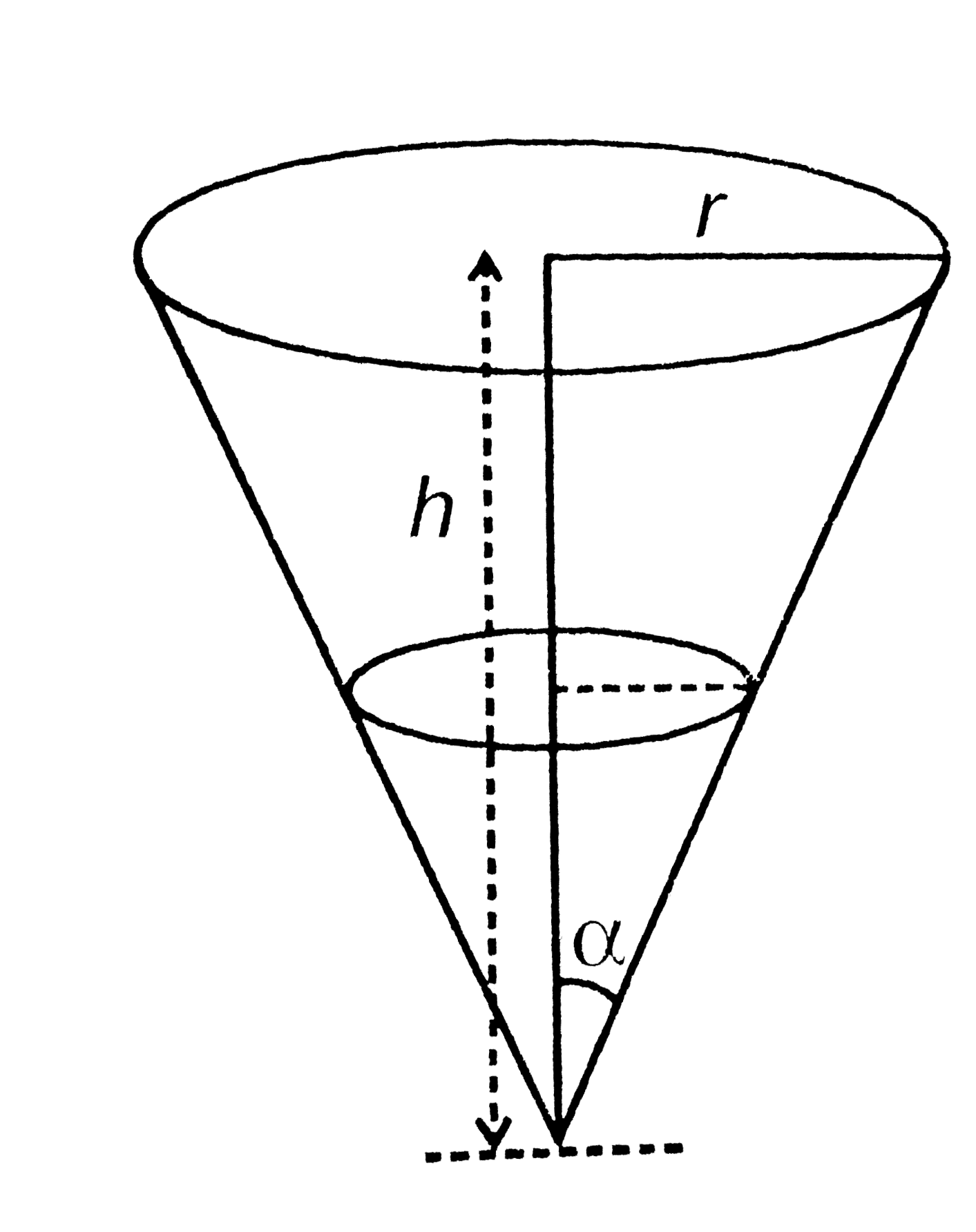
A water tank has the shape of an inverted righ circular cone with its axis vertical and vertex lowermost . Its semi-vertical angle is . Water is poured into it at a constant rate of 4 cubic meter per hour . Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 2 m.
m/h
m/h
m/h
m/h
The correct Answer is:A
Let r, h and be as in Fig. Then .
So,
But (given )
Let V be the volume of the cone. Then
Therefore (by Chain Rule )
Now rate of change of volume , i.e., and h=2m
Therefore ,
Thus , the rate of change of water level is
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBook:AAKASH INSTITUTEChapter:APPLICATION OF DERIVATIVESExercise:TRY YOURSELF
Explore 39 Videos
- APPLICATION OF DERIVATIVESBook:AAKASH INSTITUTEChapter:APPLICATION OF DERIVATIVESExercise:Assignment SECTION-A (Competition Level Questions)
Explore 50 Videos
- APPLICATION OF INTEGRALS Book:AAKASH INSTITUTEChapter:APPLICATION OF INTEGRALS Exercise:Assignment Section - I Aakash Challengers Questions
Explore 2 Videos
Similar Questions
A water tank has the shape of an inverted right-circular cone with its axis vertical and vertex lower most. Its semi-vertical angle is tan−1(12). Water is poured into it at a constant rate of 5 cubic meter per minute. Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 10 m.
View SolutionA water tank has a shape of an inverted right circular cone with its axis vertical and vertex lowermost. Its semi-vertical angle is tan−1(34) . Water is poured into it at a constant rate of 3 cubic meter per hour.The rate at which the level of the water is rising at an instant when the depth of water in the tank is 4m is
View Solution
Knowledge Check
A water tank has the shape of an inverted right circular cone, whose semi-vertical angle is tan−1(12). Water is poured into it at a constant rate of 5 cu m/min. Then, the rate (in m/min) at which the level of water is rising at the instant when the depth of water in the tank is 10 m is
A2πB15πC115πD110π
A water tank has a shape of an inverted right circular cone with its axis vertical and vertex lower-most. Its semi-vertical angle is tan−1(34) . Water is poured into it at a constant rate of 3 cubic meter per hour. The rate at which the level of the water is rising at an instant when the depth of water in the tank is 4m is
View SolutionA water tank has the shape of an inverted right - circular cone with its axis vertical and vertex lower most. Its semi - vertical angle is tan−1(12). Water is poured into it at a constant rate of 5 cubic meter per minute. Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 10 m.
View SolutionA water tank has the shape of an inverted right circular cone with its axis vertical and vertex lowermost. Its semi-vertical angle is tan−1(0.5). Water is poured into it at a constant rate of 5 cubic metre per minute. Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 10m.
View SolutionA water tank has the shape of a cube with each side of length 3 metre. Water is poured into it at a constant rate of 27 cubic metre per hour. Then,the rate at which the level of the water is rising at the instant, when the depth of water in the tank is x,(0<x<2), is (in metre per hour) (i)x (ii) 3x (iii) 9x (iv) 3
View SolutionAn inverted cone has a depth of 40 cm and a base of radius 5 cm. Water is poured into it at a rate of 1.5 cubic centimetres per minutes. Find the rate at which the level of water in the cone is rising when the depth is 4 cm
View SolutionThe bottom of a rectangular swimming tank is 25 m by 40m. Water is pumped into the tank at the rate of 500 cubic metres per minute. Find the rate at which the level of water in the tank is rising.
View SolutionAn inverted cone has a depth of 10cm and a base of radius 5cm. Water is poured into it at the rate of 3/2 c.c. per minute. Find the rate at which the level of water in the cone is rising when the depth is 4cm.
View Solution