Prove that function given by f(x)=sin x is
(i) Strictly increasing in (−π2,π2)
(ii) Strictly decreasing in (π2,3π2)
f(x)=sinx
then , f'(x)=cosx
(i) For each x∈(−π2,π2)
cosx>0
So, f'(x)>0
f(x) is strictly increasing in (−π2,π2)
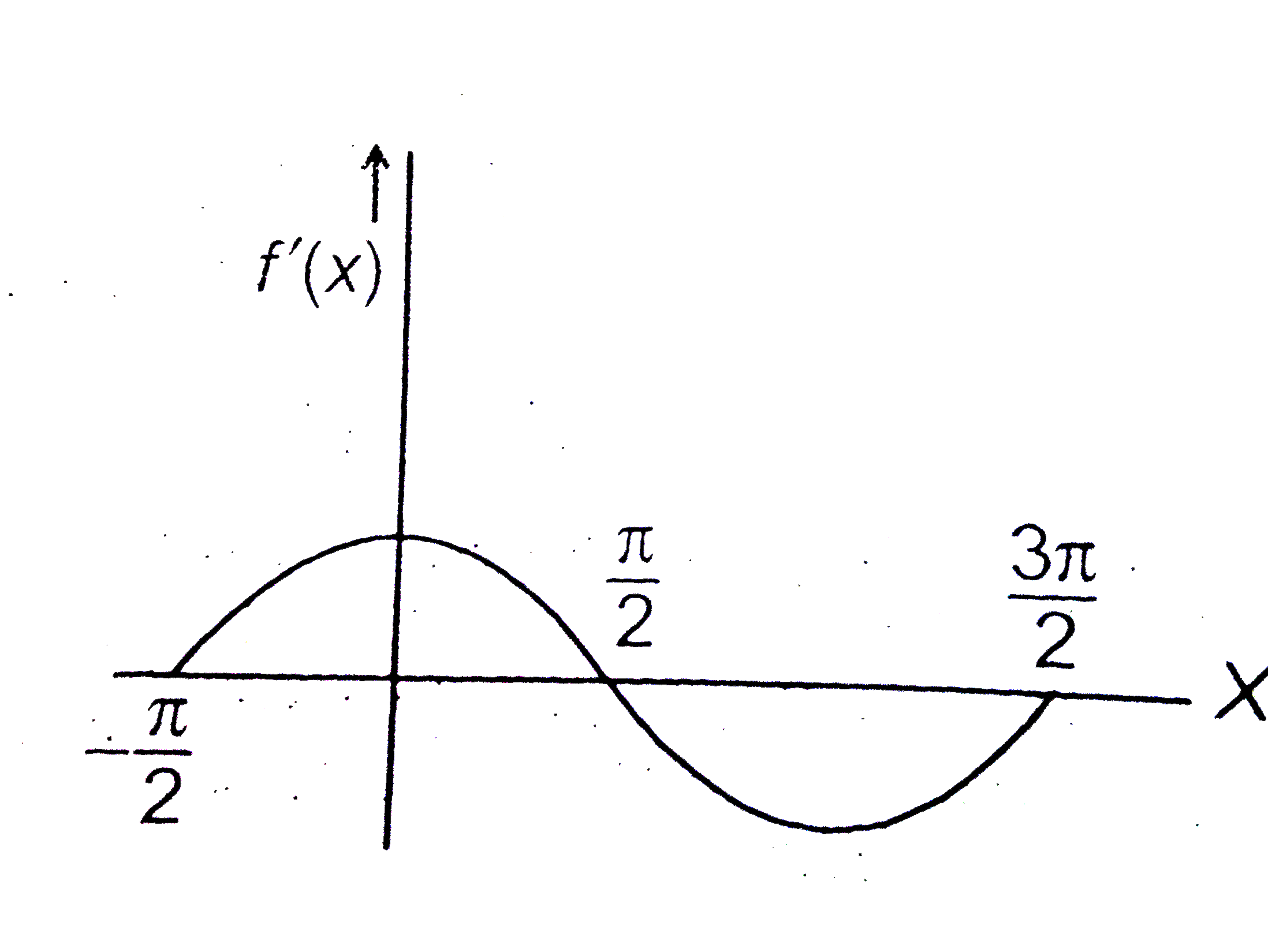
(ii) For each x∈(π2,3π2)
cosx<0
So, f'(x)<0
f(x) is strictlyu decreasing in x∈(π2,3π2)
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - AAKASH INSTITUTECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - TRY YOURSELF
39 Videos
- APPLICATION OF DERIVATIVESBOOK - AAKASH INSTITUTECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Assignment SECTION-A (Competition Level Questions)
50 Videos
- APPLICATION OF INTEGRALS BOOK - AAKASH INSTITUTECHAPTER - APPLICATION OF INTEGRALS EXERCISE - Assignment Section - I Aakash Challengers Questions
2 Videos
Similar Questions
Prove that the function 'f' given by f(x)=logsinx is strictly increasing on (0,π2) .
View SolutionShow that the fucntion given by f(x)=sinx is :
(a) strictly increasing in (0,π2)
(b) strictly decreasing in (π2,π)
(c ) neither increasing nor decreasing in (0,π).
View SolutionProve that the function f given by f(x)=logcosx is strictly decreasing on (0,π2) .
View SolutionProve that the function f given by f(x)=log(cosx) is strictly increasing on (−π2,0)and strictly decreasing on(0,π2)
View SolutionProve that the function f given by f(x)=logsinxf(x)=logsinxis strictly increasing on (0,π2)and strictly decreasing on (π2,π).
View SolutionProve that the function f given by f(x)=logcosx is strictly increasing on (−π/2, 0) and strictly decreasing on (0, π/2) .
View SolutionProve that the function f(x)=cosx is strictly increasing in (π, 2π)
View SolutionProve that the function given by f(x)=2x3−6x2+7x is strictly increasing in R.
View Solutionshow that the function f(x)=sinx is strictly increasing in (0,π2) strictly decreasing in (π2,π)
View SolutionShow that the function given by f(x)=sinx is
(a) strictly increasing in (0,π2) (b) strictly decreasing in (π2,π)(c) neither increasing nor decreasing in (0,π)
View Solution
