Find the distances of the point P(2, 3, 2) from the
coordinate planes.
The distance between the point and XY-plane is
equal to z-coordinate.
Hence, distance between the point and XZ and YZ-planes are 3 units and 2 units
respectively. 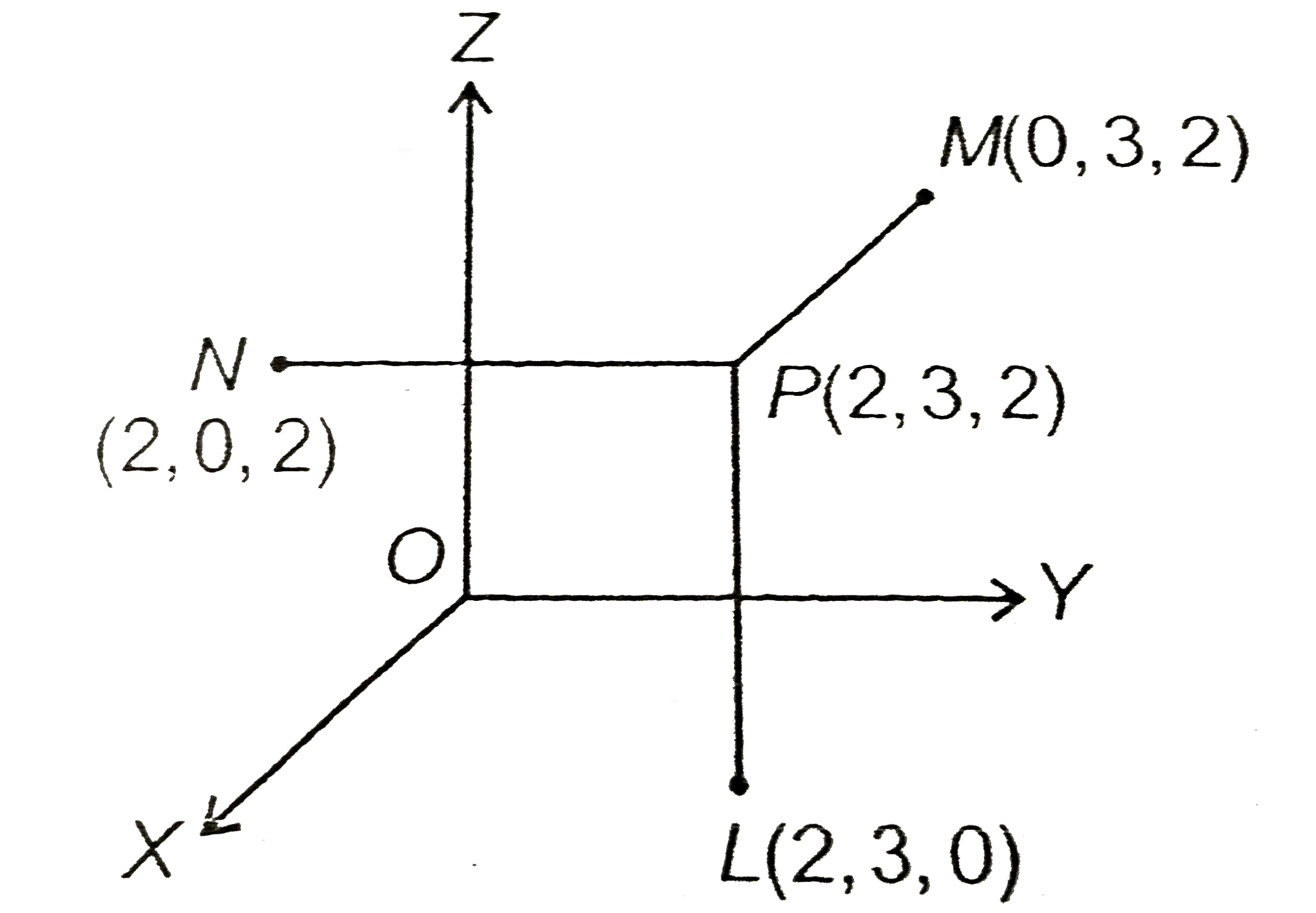
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - Illustration4videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - TRY YOURSELF97videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTECHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)5videos
STRAIGHT LINES
- BOOK - AAKASH INSTITUTECHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)15videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
Find the distances of the point (-4, -3, 4) from the coordinate planes.
[Hint : Distance cannot be negative.]View SolutionFind the distances of the point (-4, 3, 6) from the coordinate planes.
[Hint : Distance cannot be negative.]View SolutionFind the distances of the point P(−4,3,5) from the coordinate axes.
View SolutionFind the distance of the point (2, 3, 5) from the xy-plane.
View SolutionFind the distance of the point P (1,2,3) from its image in the plane x + 2y + 4z = 38.
View SolutionWrite the distance of the point P(2,3,5) from the xy-plane.
View SolutionFind the distance of the point P(a,b,c) from x−y plane.
View SolutionFind the distance of the point (2, 3, -5) from the plane x+2y−2z−9=0.
View SolutionFind the distance of the point (2,3,-5) from the plane x+2y−2z=9.
View SolutionFind the distance of the point P(–1, –5, –10) from the point of intersection of the line joining the points A(2, –1, 2) and B(5, 3, 4) with the plane x – y + z = 5.
View Solution

