If mid-points of the sides of a triangle are (1, 2, -3), (3, 0, 1) and (-1, 1, -4). Find its vertices.
Let A(x1,y1,z1),B(x2,y2,z2)andC(x3,y3,z3) be the vertices of the given triangle, and let
D(1, 2, -3), E(3, 0, 1) and F(-1, 1, -4) be the mid-points of the sides AB, AC and BC respectively.
Now D is the mid-point of AB
⇒x1+x22=1,y1+y22=2,z1+z22=−3
⇒x1+x2=2…(i)
⇒y1+y2=4…(ii)
and z1+z2=−6…(iii)
E is the mid-point of AC
⇒x1+x32=3,y1+y32=0,z1+z32=1
⇒x1+x3=6...(iv)
y1+y3=0…(v)
and z1+z3=2...(vi)
F is the mid- point of BC
⇒x2+x32=−1,y2+y32=1,z2+z32=−4
⇒x2+x3=−2…(vii)
y2+y3=2…(viii)
and z2+z3=−8…(ix)
On adding (i), (iv), and (vii), we get ___
2(x1+x2+x3)=6
⇒x1+x2+x3=3...(x)
On solving (i), (iv), and (vii) with (x), we get
x1=5,x2=−3,x3=1 On adding (ii), (v) and (viii), we get
2(y1+y2+y3)=6
⇒y1+y2+y3=3 ...(xi)
On solving (ii), (v) and (viii) with (xi), we get
y1=1,y2=3,y3=−1
On adding (iii), (vi) and (ix), we get
2(z1+z2+z3)=−12
⇒z1+z2+z3=−6 … (xii)
On solving (iii), (vi) and (xi) with (xii), we get
z1=2,z2=−8,z3=0
Hence, the vertices of the triangle are A(5, 1, 2), B(-3, 3, -8) and C(1, -1, 0).
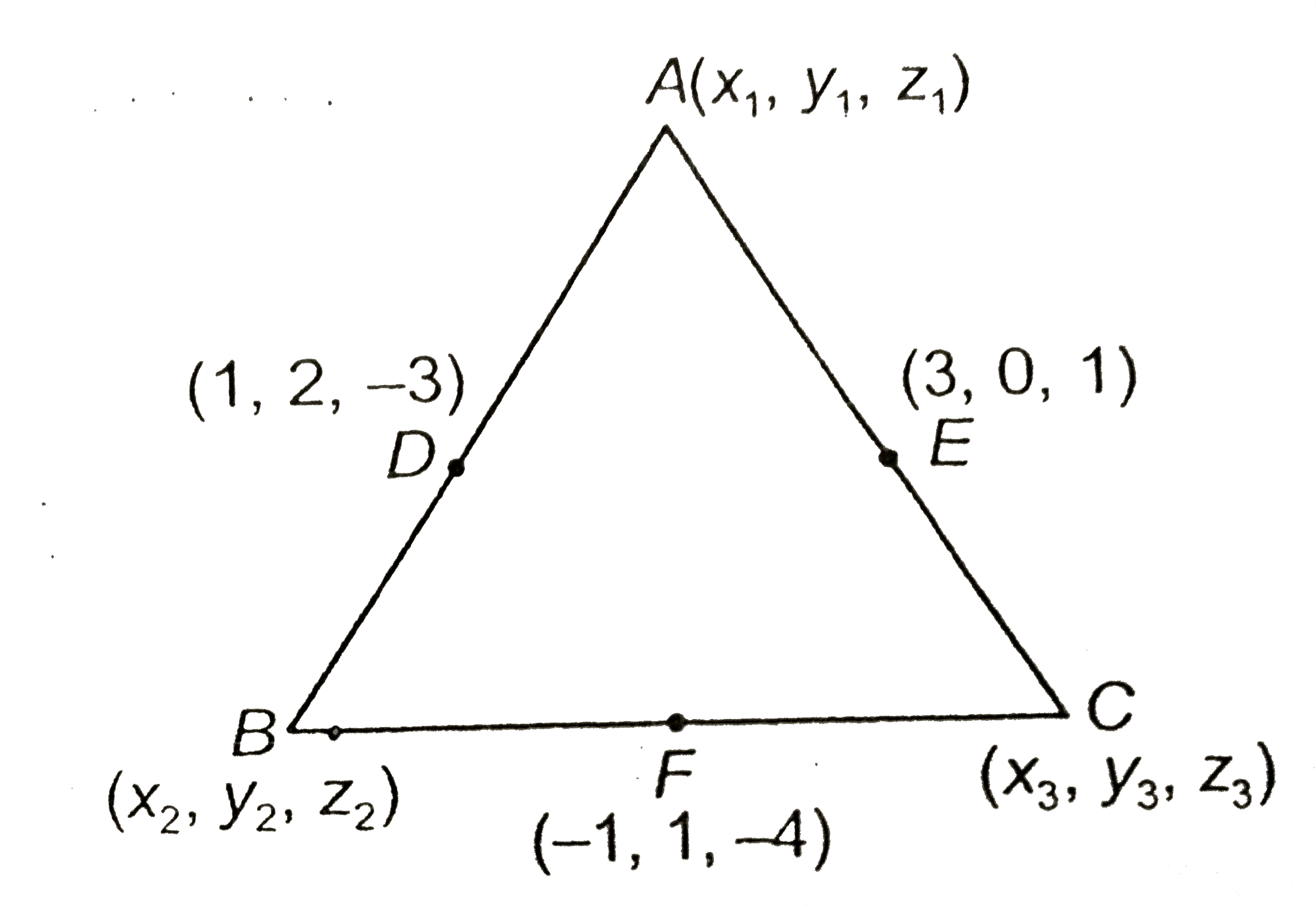
Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRY Book:AAKASH INSTITUTEChapter:THREE DIMENSIONAL GEOMETRY Exercise:Illustration
Explore 4 Videos
- THREE DIMENSIONAL GEOMETRY Book:AAKASH INSTITUTEChapter:THREE DIMENSIONAL GEOMETRY Exercise:TRY YOURSELF
Explore 97 Videos
- STRAIGHT LINESBook:AAKASH INSTITUTEChapter:STRAIGHT LINESExercise:SECTION-J (AAKASH CHALLENGERS QUESTIONS)
Explore 5 Videos
- TRIGNOMETRIC FUNCTIONS Book:AAKASH INSTITUTEChapter:TRIGNOMETRIC FUNCTIONS Exercise:Section - J (Akash Challengers Question)
Explore 15 Videos
Similar Questions
Knowledge Check
It the mid-points of the sides of triangle are (1, 2, -3),
(3, 0, 1) and (2, -2, 5), then the centroid isA(0, 0, 0)B(1, 2, 3)C(2, 0, 1)D(2, 3, 0)If the coordinates of the mid points of the sides of a triangle are (1,1) ,(2,-3) and (3,4) . Find its centroid :
A(3, 2/3)B(2, 3/4)C(2, 2/3)Dnone of these
The mid- points of the sides of a tiangle are (1,5,-1) (0,4,-2) and (2,3,4) . Find its vertices and also find the centroid of the triangle.
View SolutionIf the coordinates of the mid-points of the sides of a triangle are (3,4),(4,6)and(5,7), find its vertices.
View SolutionIf the coordinates of the mid-points of the sides of a triangle are (1,1),(2,−3)and(3,4) . Find its centroid.
View SolutionThe mid-points of the sides of a triangle are given by (3, 2, -4), (9, 8, -15) and (5, 4, 6). Find
the coordinates of its vertices.
View SolutionThe mid point of the sides of a triangle are (1,5,-1) (0,4,-2) and (2,3,4) find its vertices also find the centroid of the triangle
View Solutionif the coordinates of the mid points of the Sides of a triangle are (1,2),(0,−1) and (2,−1).Find the coordinates of its vertices :
View Solution
