(i) Find the angle bewteen the lines whose direction ratios are 1, 2, 3 and - 3 , 2 , 1
(ii) Find the angle between two diagonals of a cube.

Video Solution

Text Solution

Verified by Experts

(i) Let $θ$ be the required angle , themn
$cos θ = \frac{1 \times - 3 + 2 \times 2 + 3 \times 1}{\sqrt{1 + 4 + 9} \sqrt{1 + 4 + 9}} = \frac{4}{14} = \frac{2}{7}$
$\Rightarrow θ = {cos}^{- 1} (\frac{2}{7})$
(ii) From the adjoining figure, the direction rations of the diagonals OP and CD of a given cube ltbgt are given by
$a - 0, a - 0, a - 0$ and
$a - 0, a - 0, 0 - a$

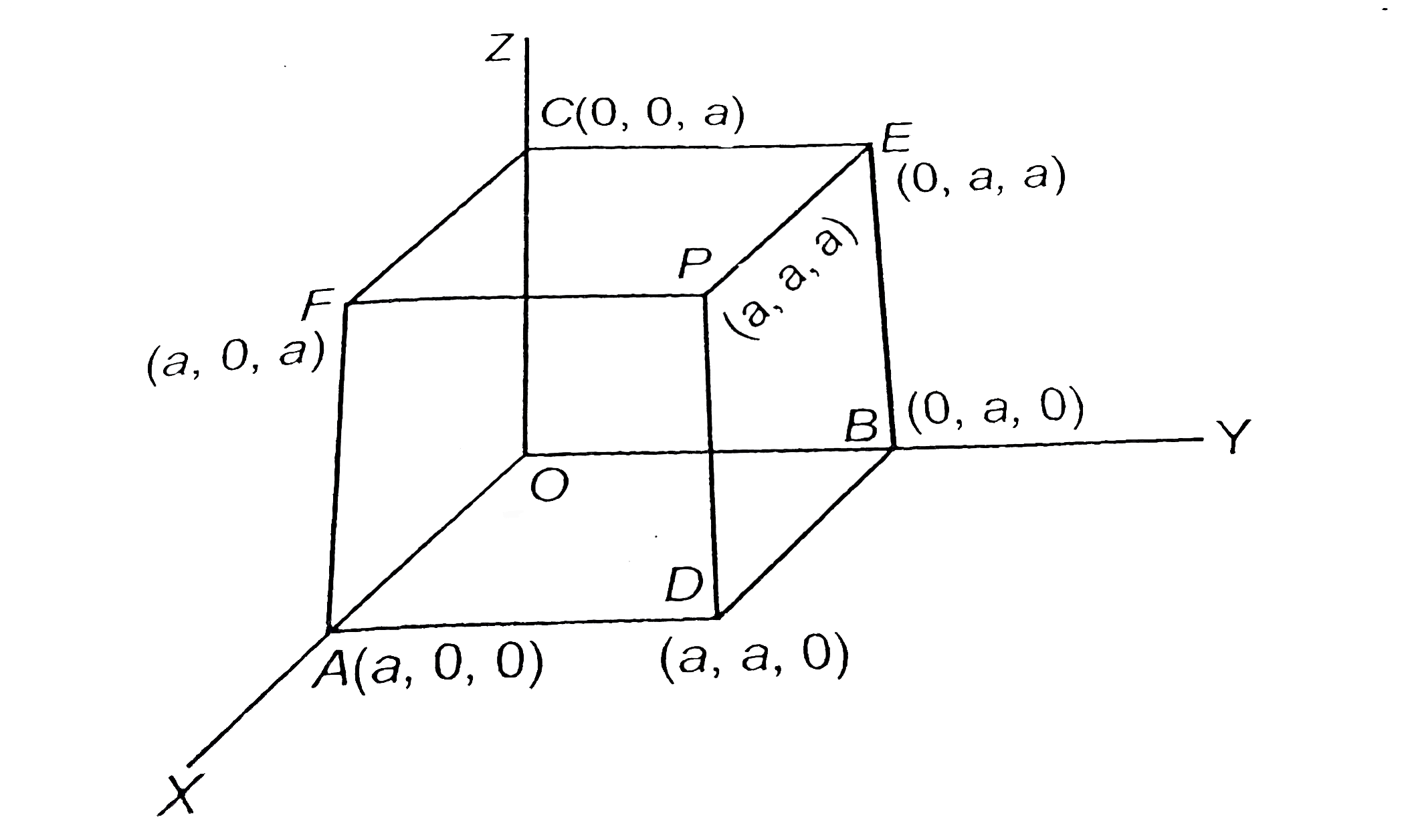
and hence their respective direction cosines are
$- \frac{a}{\sqrt{a^{2} + a^{2} + a^{2}}}, \frac{a}{\sqrt{a^{2} + a^{2} + a^{2}}}, \frac{a}{\sqrt{a^{2} + a^{2} + a^{2}}} i . e ., \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}$
and $\frac{a}{\sqrt{a^{2} + a^{2} + a^{2}}}, \frac{a}{\sqrt{a^{2} + a^{2} + a^{2}}}, \frac{- a}{\sqrt{a^{2} + a^{2} + a^{2}}} i . e ., \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{- 1}{\sqrt{3}}$
Let $θ \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} + \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, + \frac{1}{\sqrt{3}}, \frac{- 1}{\sqrt{3}} = \frac{1}{3} + \frac{1}{3} - \frac{1}{3} = \frac{1}{3}$
$\Rightarrow θ {cos}^{- 1} (\frac{1}{3})$

Updated on:21/07/2023

The angle between two diagonals of a cube İs
A ${cos}^{- 1} (\frac{1}{3})$
B $30^{\circ}$
C ${cos}^{- 1} (\frac{1}{\sqrt{3}})$
D $45^{\circ}$
The acute angle between the lines whose direction ratios are 1, 2, 2 and -3, 6, -2 is
A ${cos}^{- 1} (\frac{13}{21})$
B ${cos}^{- 1} (\frac{5}{21})$
C ${cos}^{- 1} (\frac{11}{21})$
D ${cos}^{- 1} (\frac{5}{9})$
The acute angle between the lines whose direction ratios are 3, 2, 6 and -2, 1, 2 is
A ${cos}^{- 1} (\frac{8}{21})$
B ${cos}^{- 1} (\frac{12}{21})$
C ${cos}^{- 1} (\frac{2}{21})$
D ${cos}^{- 1} (\frac{2}{3})$