If →a,→b,→c,→d are the position vectors of the verticles of a cyclic quadrilateral ABCd prove that
∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d×→b∣∣(→b−→c).(→d−→c)=0
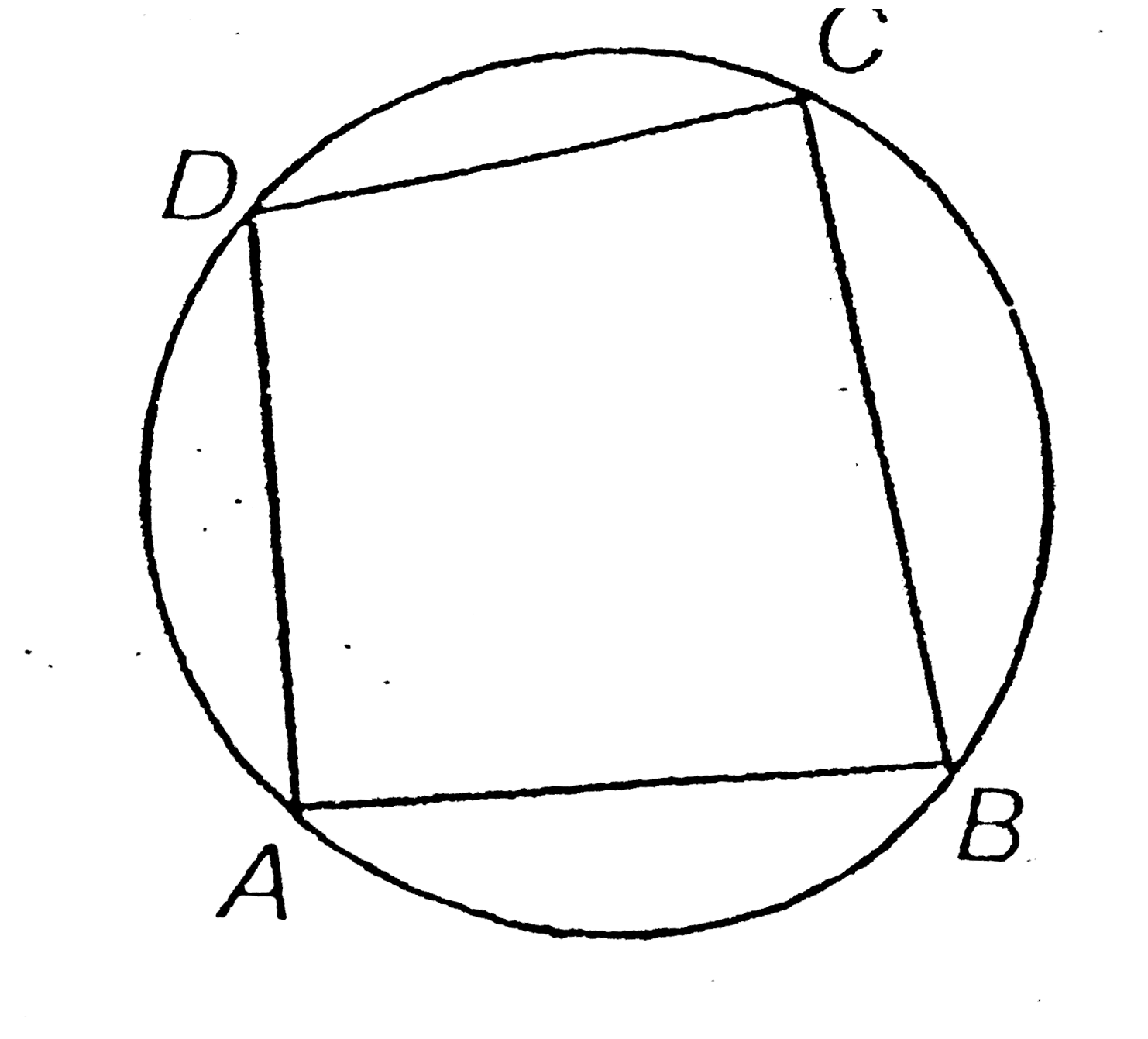
Consider ∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)
We have,
(→a−→d)×(→b−→a)
=→a×→b−→a×→a−→d×→b+→d×→a
=→a×→b+→b×→d+→d×→a
∴∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)=∣∣(→a−→d)×(→b−→a)∣∣(→b−→a).(→d−→a)
=∣∣→a−→d∣∣∣∣→b−→a∣∣sinA∣∣→b−→a∣∣∣∣→d−→a∣∣cosA=tanA
Again, ∣∣→b×→c+→a×→d+→d×→b∣∣(→b−→c).(→d−→c)=∣∣(→b−→c)×(→c−→d)∣∣(→b−→c):(→d−→c)
=∣∣→b−→c∣∣∣→c−→dsinC∣∣→b−→c∣∣∣∣→d−→c∣∣cosC=tanC
in a cyclic quadrilateral A+C=π⇒A=π−C
⇒tanA=tan(π−C)
⇒tanA=−tanC
⇒tanA+tanC=0
⇒∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d×→d∣∣(→b−→c).(→d−→c)=0
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - AAKASH INSTITUTECHAPTER - VECTOR ALGEBRAEXERCISE - ILLUSTRATION
1 Videos
- VECTOR ALGEBRABOOK - AAKASH INSTITUTECHAPTER - VECTOR ALGEBRAEXERCISE - TRY YOURSELF
20 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTECHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
15 Videos
Similar Questions
If →a,→b,→cand→d are the position vectors of the vertices of a cycle quadrilateral ABCD, prove that ∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d+→d×→b∣∣(→b−→c).(→d−→c)
View SolutionIf →a,→b,→cand→d are the position vectors of the vertices of a cycle quadrilateral ABCD, prove that ∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d+→d×→b∣∣(→b−→c).(→d−→c)
View Solution
Knowledge Check
If →a,→b,→c,→d are coplanar vectors, then (→a×→b)×(→c×→d)=
A1B→aC→bD→0
Prove that: [(→a×→b)×(→a×→c)].→d=[→a→b→c](→a.→d)
View SolutionProve that: (→a×→b)×(→c×→d)+(→a×→c)×(→d×→b)+(→a×→d)×(→b×→c)=2[→b→c→d]→a
View SolutionProve that →a×{→b×(→c×→d)}=(→b.→d)(→a×→c)−(→b.→c)(→a×→d)
View SolutionProve that →a'×→b'+→b'×→c'+→c'×→a'=→a+→b+→c[→a→b→c]
View SolutionShow that: (→a−→d)×(→b−→c)+(→b−→d)×(→c−→a)+(→c−→d)×(→a−→b) is independent of →d.
View SolutionIf →a,→b,→cand→a',→b',→c' are reciprocal system of vectors, then prove that →a'×→b'+→b'×→c'+→c'×→a'=→a+→b+→c[→a→b→c]
View SolutionIf →a,→b,→c,→d are four distinct vectors satisfying the conditions →a×→b=→c×→dand→a×→c=→b×ecd then prove that →a.→b+→c.→d≠→a.→c+→b.→d
View Solution
