A straight line segment (3, 4) in the first quadrant meets the co ordinate axes in A and B. The minimum area of ΔAOB is
Step by step video & image solution for A straight line segment (3, 4) in the first quadrant meets the co ordinate axes in A and B. The minimum area of Delta AOB is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
সম্পর্কিত প্রশ্ন
A straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
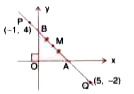
The co-ordinates of A and B.View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
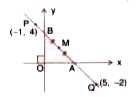
The co-ordinates of M.View SolutionIf a straight line I passing through P(3,4) meets positive co-ordinate axes at A &B such that area of triangle OAB is minimum (where O is origin) then slope of I is
View SolutionThe plane lx+my+nz=p intersects co-ordinate axes at A,B and C .If area of ΔABC is Δ ,then
View SolutionA straight line passing through P(3,1) meets the coordinate axes at AandB . It is given that the distance of this straight line from the origin O is maximum. The area of triangle OAB is equal to
View SolutionThe plane x2+y3+z4=1 cuts the co-ordinate axes in A,B,C: then the area of the ΔABC is
View SolutionThe equation of the line through (3,4) which cuts from the first quadrant a triangle of minimum area
View SolutionThe equation of the straight line passing through the point (4.3) and making intercepts on the co ordinate axes whose sum is −1, is
View SolutionThe equation of the straight line passing through the point (4.3) and making intercepts on the co ordinate axes whose sum is −1, is
View SolutionA line passing through (3,4) meets the axes ¯¯¯¯¯¯OXand¯¯¯¯¯¯OYatAandB respectively. The minimum area of the triangle OAB in square units is
View Solution

