A(0,a),B(0,b) be fixed points. P(x,0) a variable point. The angle ∠APB is maximum
Step by step video & image solution for A(0, a), B(0, b) be fixed points. P(x, 0) a variable point. The angle angle APB is maximum by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A and B are two fixed points. The locus of a point P such that ∠APB is a right angle, is:
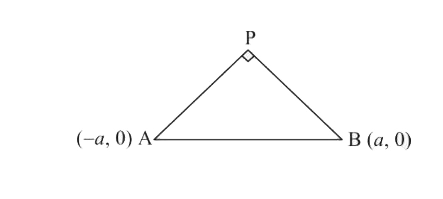 Ax2+y2=a2Bx2−y2=a2C2x2+y2=a2DNone of these
Ax2+y2=a2Bx2−y2=a2C2x2+y2=a2DNone of these
A(1, 2) and B(7, 10) are two points. If P(x) is a point such that the angle APB is 60∘ and the area of the triangle APB is maximum, then which of the following is (aré) true? a) P lies on the straight line 3x+4y= 36 b) P lies on any line perpendicular to AB
View SolutionA(1, 2) and B(7, 10) are two points. If P(x) is a point such that the angle APB is 60∘ and the area of the triangle APB is maximum, then which of the following is (aré) true?
View SolutionLet π be the plane parallel to y-axis and containing the points (1,0,1) and (3,2,-1). Also A=(4,0,0)andB=(6,0,−2) are two points and P=(x0,y0,z0) is a variable point on the plane π=0.
View SolutionA and B are two fixed points. Draw the locus of a point P such that angle APB=90∘.
View SolutionA and B are two fixed points. The locus of a point P such that ∠APB is a right angle, is:

View SolutionIf A and B are two fixed points and P is a variable point such that PA+PB=4, the locus of P is
View SolutionIf A and B are two fixed points and P is a variable point such that PA+PB=4, the locus of P is
View Solution
