If I is the incenter of the circle inscribed in the triangle ABC and AI cuts BC at P, then
APSinC=bsin(B+A2)
(AP)=bSinCSin(B+A2)
AI=rSinA2
rcotA2+rcotB2=C
r=CcotA2+CotB2
r=CSina2⋅Sinb2Cos(C2)
We need to find the ratio of AI and AP
AIAP=C⋅sinB2CosC2⋅Sin(B+A2)bSinC
=cb⋅sinB2⋅sin(B+A2)CosC2SinC
=Sin(B+A2)2⋅cosB2CosC2
=2⋅CosA2⋅Sin(B+A2)SinA+SinB+SinC
=SinC+SinBSinA+SinB+SinC
=b+ca+b+c
Option a is correct.
Similar Questions
If f is the centre of a circle inscribed in a triangle ABC, then ∣∣∣−−→BC∣∣∣−→IA+∣∣∣−−→CA∣∣∣−→IB+∣∣∣−−→AB∣∣∣−→IC is
View SolutionLet ABC be an isosceles triangle with base BC whose length is 'a'. If 'r ' is the radius of the circle inscribed in the ΔABCandr1 be theradius of the circle escribed opposite to the angle A, then the product rr1 can be equal to
View Solution
Knowledge Check
If I is the centre of a circle inscribed in a triangle ABC, then ∣∣→BC∣∣→IA+∣∣→CA∣∣→IB+∣∣→AB∣∣→IC is
A→0B→IA+→IB+→ICC→IA+→IB+→IC3Dnone of theseIn a right triangles ABC right angled at B,BC = 12 cm and AB = 5 cm . The radius of the circle inscribed in the triangle (in cm) is
A4B3C2D1if an equilateral triangle ABC with vertices at z1,z2andz3 be inscribed in the circle |z|=2 and again a circle is inscribed in the triangle ABC touching the sides AB, BC and CA at D(z4),E(z5)andF(z6) respectively
 APQRS4123BPQRS3412CPQRS1324DPQRS2134
APQRS4123BPQRS3412CPQRS1324DPQRS2134
If I is the centre of a circle inscribed in a triangle ABC, then ∣∣∣−−→BC∣∣∣−→IA+∣∣∣−−→CA∣∣∣−→IB+∣∣∣−−→AB∣∣∣−→IC is
View SolutionA circle with centre P is inscribed in the △ ABC. Side AB, side BC and side AC touch the circle at points L,M and N respectively. Radius of the circle is r. Prove that: A(△ABC)=12(AB+BC+AC)×r.
View SolutionIf I is the incenter of a triangle ABC, then the ratio IA IB IC is equal to
View SolutionABC is a right triangle in which ∠B=90∘. If AB=8 cmandBC=6 cm. find the diameter of the circle inscribed in the triangle.
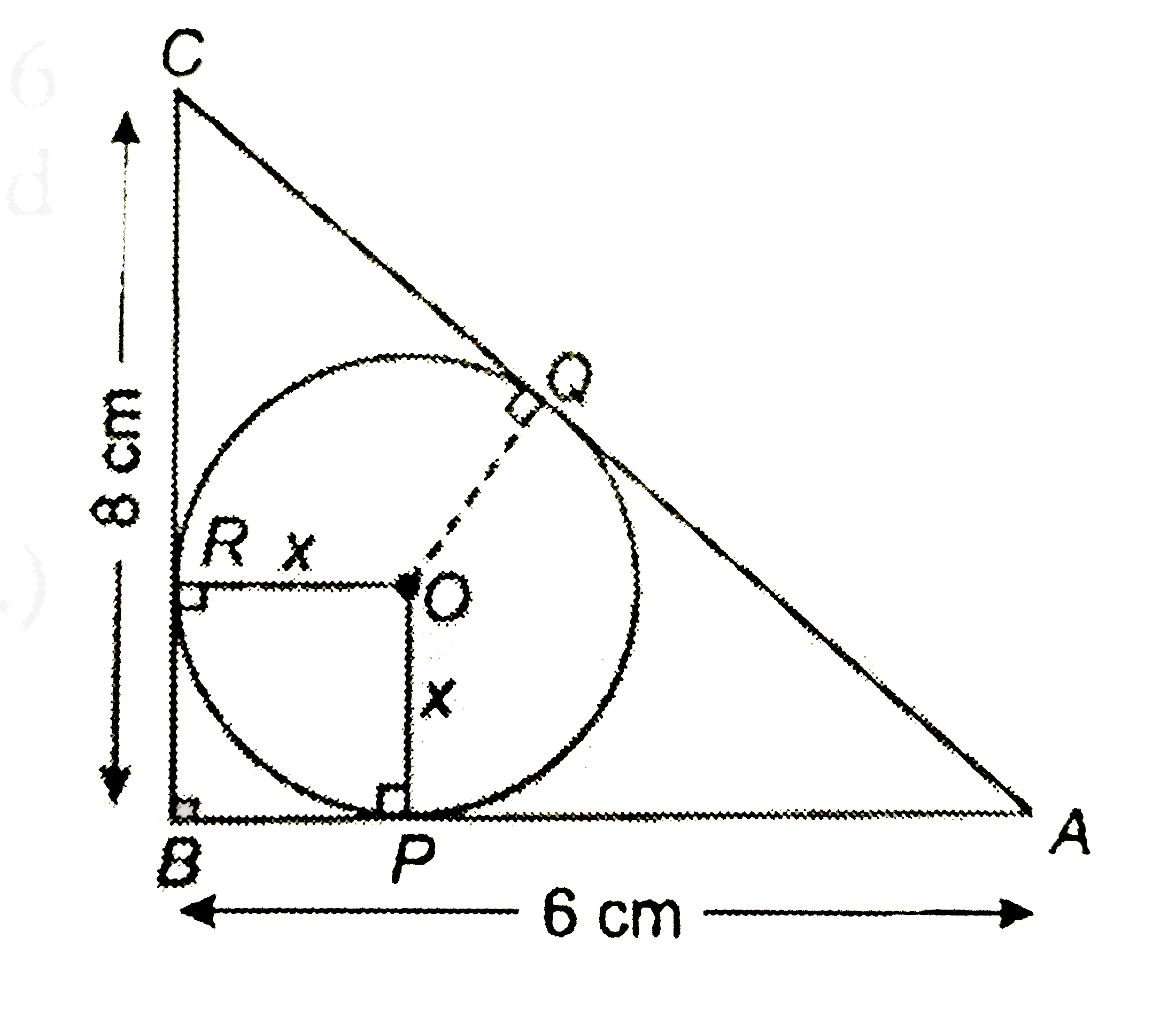
View SolutionIn the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
View Solution
