The initial speed of an arrow shot from a bow, at an elevation of 30∘, is 15ms–1. Find its velocity when it hits the ground back
Here v015 m s−1, angle of projection , θ0=30∘
Therefore, v0x=v0cosθ_(0)
=15cos(30∘)
=15√32 m s−1
And v0y=v0sinθ0
=152ms−1
Horizontal component of velocity remians constant throughout the fight i.e.
vx=v0x=15√32ms−1
Vertical component of velocity is given by
vy=v0sinθ0−>
Put t=Tf=2v0sinθ0g
⇒vy=v0sinθ0−g×2v0sinθ0g
vy=−v0sinθ0
1vy−152ms−1
Thus, total velocity v=√v2x+v2y
√152×34+1524⎞⎠
v=15ms−1
Let the final velocity make and angle θ with the positive x - axis , then
tetha=tan−1(vyvx)
θ=tan−1⎛⎜⎝−15215√32⎞⎟⎠
=tan−1(−1√3)
θ=−30∘
(##AAK_T1_PHY_C02_SLV_029_S01.png" width="80%">
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A PLANEEXERCISE - llustration 1 :1videos
MOTION IN A PLANE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A PLANEEXERCISE - Try yourself48videos
MOTION IN A PLANE
- BOOK - AAKASH INSTITUTECHAPTER - MOCK_TEST_17EXERCISE - Example15videos
MOCK_TEST_17
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)15videos
MOTION IN A STRAIGHT LINE
Similar Questions
Knowledge Check
- Question 1 - Select One
If a projectile is projected with initial speed u and angle θ from horizontal then what will be its average power up to time when it will hit the ground again ?
A100B200C300D0 - Question 2 - Select One
From the top of a tower of height 40m, a ball is projected upward with a speed of 20ms−1 at an angle of elevation of 30∘. Then the ratio of the total time taken by the ball to hit the ground to the time taken to ball come at same level as top of tower.
A2:1B3:1C3:2D4:1 - Question 3 - Select One
A man standing on the edge of a cliff throws a stone straight up with initial speed (u) and then throws another stone straight down with same initial speed and from the same position. Find the relation of the speeds. The stones would have attained when they hit ground at the base of the cliff.
A85 mB60 mC40 mDcan't be determined
When an arrow is shot from a bow, it has kinetic energy. From where does it get the kinetic energy ?
View SolutionA projectile projected with initial velocity 20m/s and at and angle of 30∘ from horizontal. Find the total work done when it will hit the ground.
 View Solution
View SolutionA body is projected horizontally from the top of a tower with initial velocity 18ms−1. It hits the ground at angle 45∘. What is the vertical component of velocity when it strikes the ground ?
View SolutionAn aeroplane is flying vertically upwards. When it is at a height of 1000m above the ground and moving at a speed of 367m/s., a shot is fired at it with a speed of 567 ms−1 from a point directly below it. What should be the acceleration of aeroplane so that it may escape from being hit?
View Solution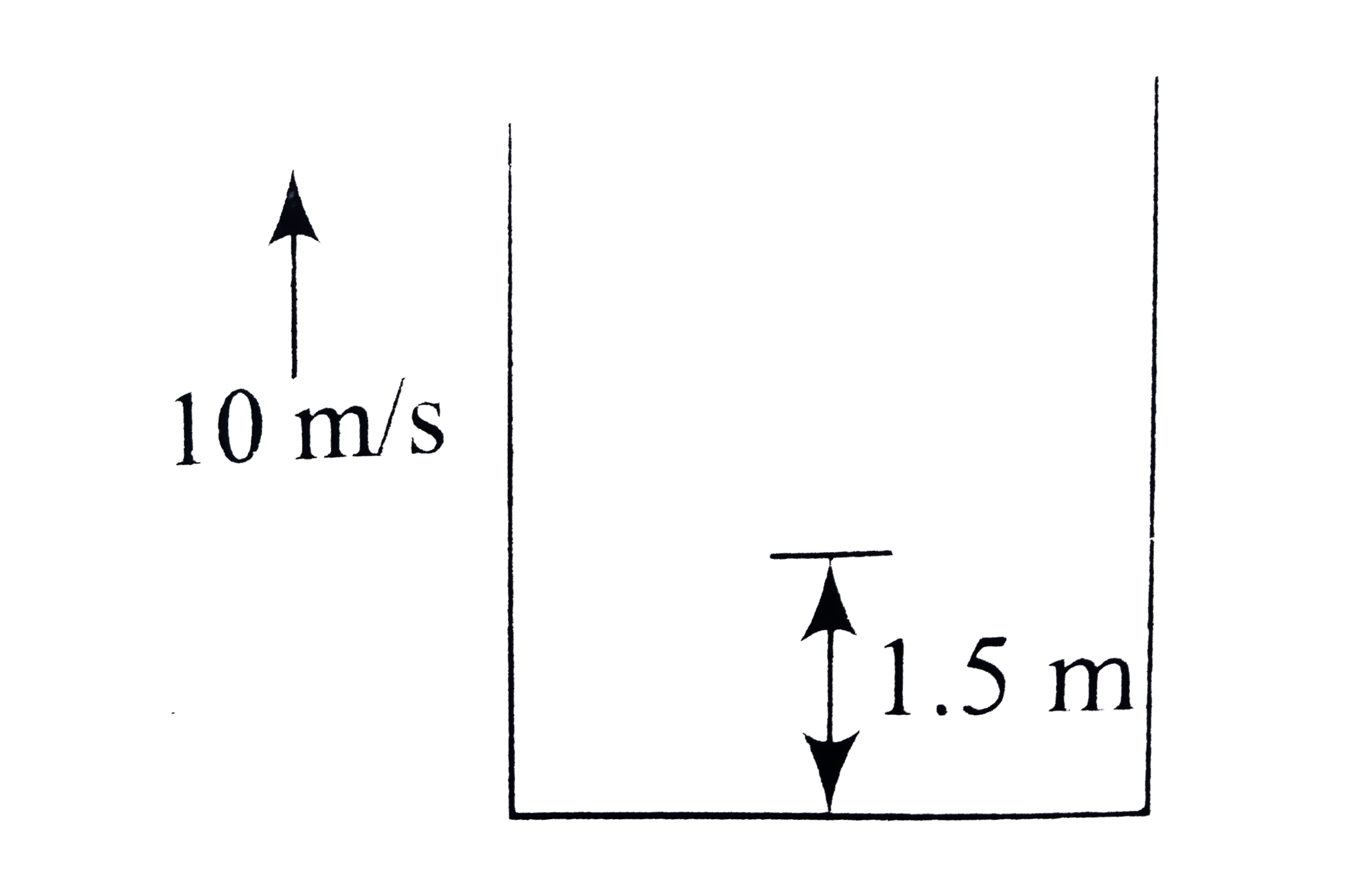
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the maximum height reached by the bullet relative to the ground :View Solution

