A coiaxial cable consists of two thin coaxial cylinders electrically connected at one end, an inner cylindrical conducting tube of radius a carrying a steady current l which is screened by an outer cylindrical conducting sheath of radius b which provides a return path. There is no dielectric medium present.
Use Ampere's theorem to derive the total magnetic energy stored in the space between the conductors, show that the inductance of a length l of the cable is
L=μ0l2πln(ba)
In this cable (a = 5 mm, b = 10 mm, l = 1000 m) is now employed in a (resistanceless) LC circuit containing a capacitance C = 1000 μF, determine the period of oscillations (neglect the capacitance of the cable itself).
2.33 ms
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - A) (OBJECTIVE TYPE QUESTIONS)
30 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - I)
6 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTECHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION -J(Aakash Challengers Questions)
5 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
Find the total field energy of magnetic field stored per unit length inside a long cylindrical wire of radius R and carrying a current I.
View SolutionThe figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :
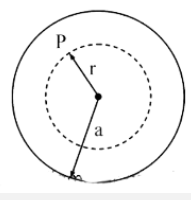
View Solution
Knowledge Check
A steady electric current is flowing through a cylindrical conductor. Then,
Athe electric field at the axis of the conductor is zeroBthe magnetic field at the axis of the conductor is zeroCthe electric field in the vicinity of the conductor is zeroDthe magnetic field in the vicinity of the conductor is zeroA cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the conductor is correctly represented by the figure:
A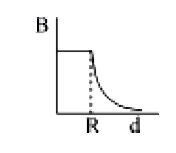 B
B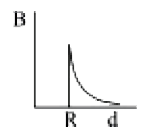 C
C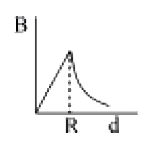 D
D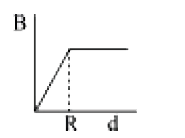
A cylindrical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
A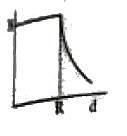 B
B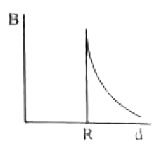 C
C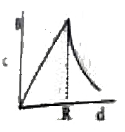 D
D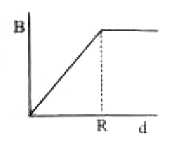
A long coaxial cable consists of two concentric cylinders of radii a and b. The central conductor of the cable carries a steady current I and the outer conductor provides the return path of the current. Calculate the energy stored in the magnetic field of length l of such a cable
View Solution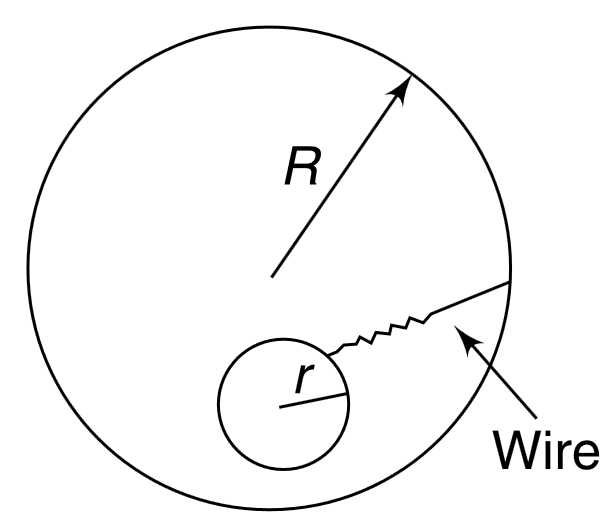
A conducting ball of radius r is charged to a potential V0. It is enveloped by a thin walled conducting sphere of radius R (gt r) and the two spheres are connected by a conducting wire. Find the potential of the outer sphere.
View SolutionWhen a steady current passes through a cylindrical conductor, is there an electric field inside the conductor?
View SolutionA cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor, is correctly represented by the figure
View SolutionA cylindrical conductor of radius R carrying current i along the axis such that the magnetic field inside the conductor varies as B=B0r2(0<r≤R), then which of the following in incorrect?
View Solution
