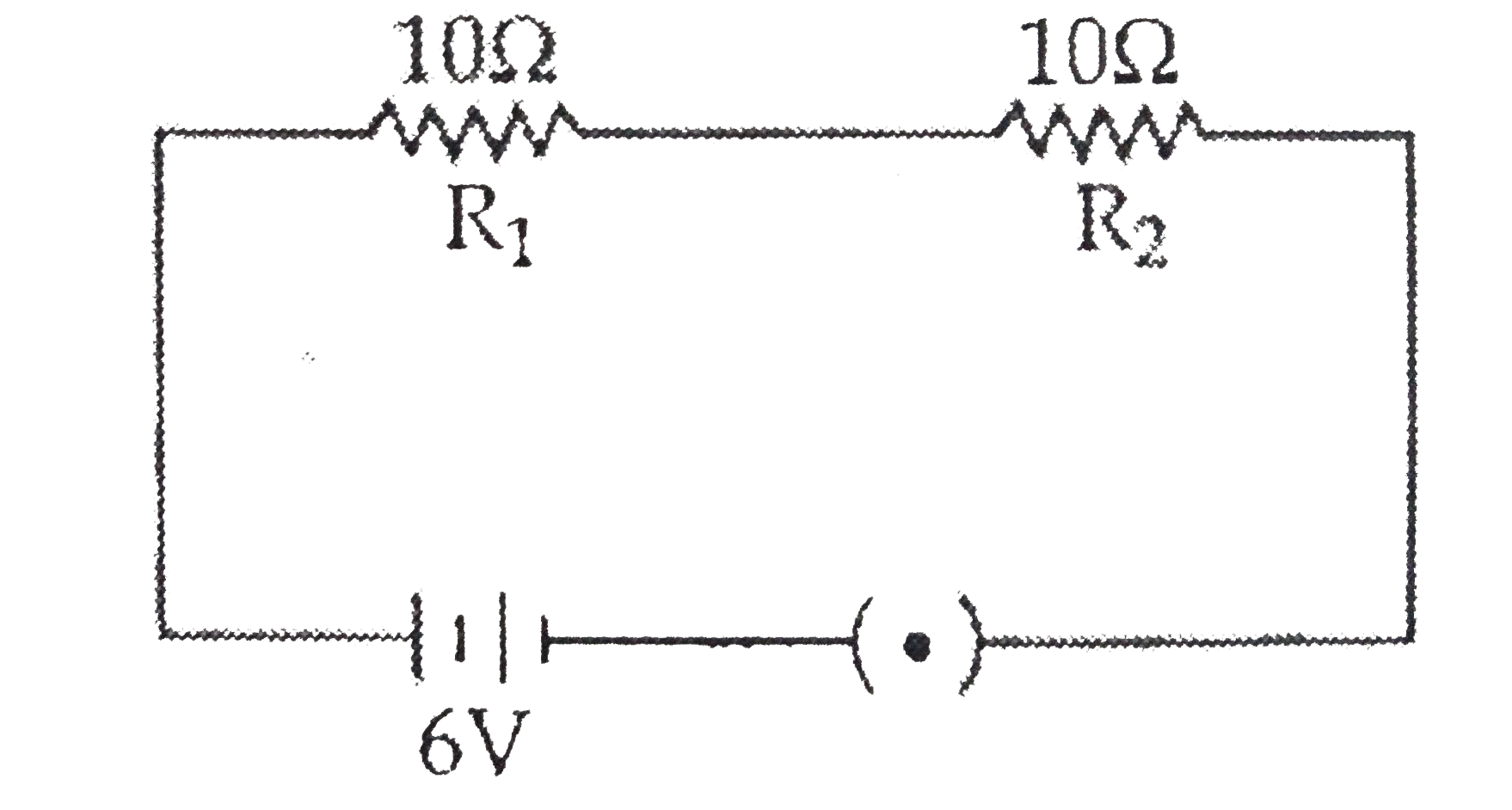
(a) Two identical resistors each of resistance 10 ohm are connected :
(i) in series.
(ii) in parallel , in terun to a battery of 6V. Calculate the ratio of power consumed in the combination of resistors in the two cases.
(b) Establish the relationship between 1 kWh and SI unit of energy .
(a) (i) Resultant resistance, R=R1+R2=10+10=20Ω
P_(1)=(V^(2))/(R)=((6)^(2))/(20)=(cancel(6)^(3)xx cancel(6)^(3))/(cancel(20)_(cancel(10)_(5)))=(9)/(5)....(i)
(ii) Resultant resistance ,R=?
(1)/(R)=(1)/(R_(1))+(1)/(R_(2))=(1)/(10)+(1)/(10)=(cancel(2)^(1))/(cancel(10)_(5))=(1)/(5)
P2=V2R=(6)25=6×65=365 ....(ii)
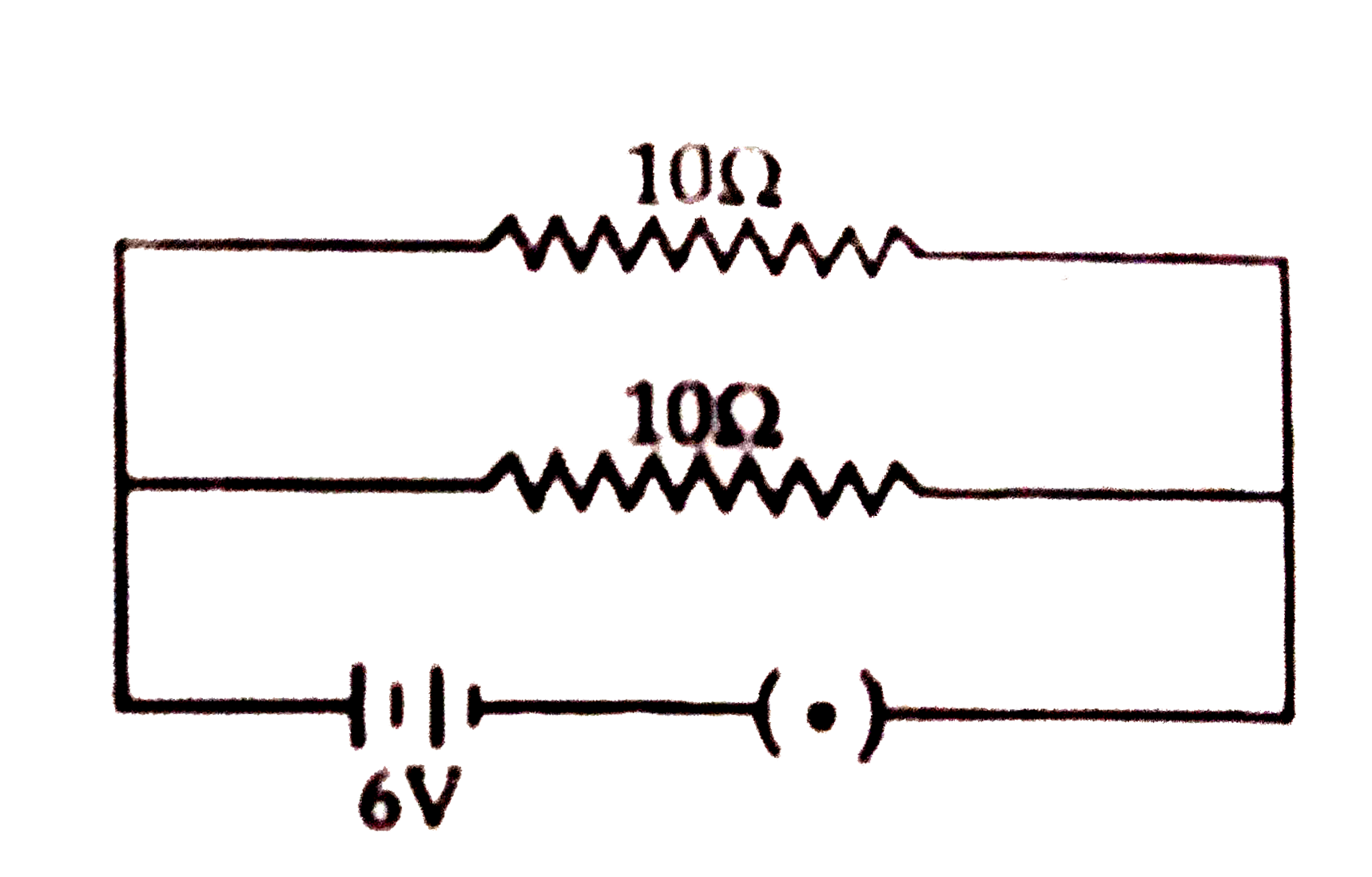
From (i) and (ii)
(P_(1))/(P_(2))=((9)/(5))/((36)/(5))=(cancel(9))/(cancel(5))xx(cancel(5))/(cancel(36)_(4))=(1)/(4)
∴P1:P2::1:4
(b) Relation between kilowatt-hour and joule (SI unit of energy ) :
1 kilowatt- hour is the amount of energy consumed at the rate of 1 kilowatt for 1 hour.
i.e., 1 kilowatt-hour = 1 kilowatt for 1 hour
or 1 kilowatt- hour =1000 watts for 1 hour
But 1 watt =1 joule 1 second
∴1 kilowatt- hour =1000 joules seconds for 1 hour
and, 1 hour =60×60 seconds
:. 1kilowa−hour= ("1000 joules")/("seconds") xx 60 xx 60seconds<br>or1kilowa−hour= 36,00,000Joe–sor3.6 xx 10^(6) J
Topper's Solved these Questions
Similar Questions
Two identical resistors each of resistance 10Ω are connected (i) in series and then (ii) in parallel, in line to a battery of 6 volts. Calculate the ratio of power consumed in the combination of resistors in the two cases.
View SolutionTwo identical resistors, each of resistance 15ohm are connected in (i) series and (ii) parallel, in turn to battery of 6V. Calculate the ratio of the power consumed in the combination of resistors in each case.
View Solution
Knowledge Check
- Question 1 - Select One
two heading coils of resistances 10Ωand20Ω are connected in parallel and connected to a battery of emf 12 V and internal resistance 1Ω Thele power consumed by the n are in the ratio
A1:4B1:3C2:1D4:1 - Question 2 - Select One
Two heating coils of resistance 10Ωand20Ω are connected in parallel and connected to a battery of emf 12V and internal resistance 1Ω. The power consumed by them is in the ratio
A1:4B1:3C2:1D4:1
Two identical resistor each of resistance 10Ω are connected in (i)series and then (ii) in parallel in line to a battery of 6 volts. Calculate the ratio of power consumed in the combination of resistor in the two case.
View SolutionTwo identical resistors, each of resistance are connected in (i) series, and (ii) parallel, in turn to a battery of 6 V. Calculate the ratio of the power consumed in the combination of resistors in each case.
View SolutionTwo identical resistors of resistance 100±5 ohm are connected parallel. Calculate the eqivalent resistance of the combination.
View SolutionTwo identical resistors are first connected in series and then in parallel. Find the ratio of equivalent resistances in two cases.
View SolutionYou take two resistors of resistance 2R and 3R and connect them in parallel in an electric circuit. Calculate the ratio of electric power consumed by 2R and 3R resistors.
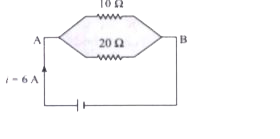
View SolutionTwo resistors of resistance 10Ω and 20Ω are connected in parallel. A battery supplies 6 A of current to the combination. Calculate the current in each resistor.
 View Solution
View Solution

