For the series combination of three resistors establish the relation :
R=R1+R2+R3
where the symbols have their usual meanings.
Calculate the equivalent resistance of the combination of three resistors of 6Ω,9Ω and 18Ω joined in parallel.
Same current (I) flows through different resistances, when these are joined I series , as shown in the figure.

Let R be the combined resistance
Then, V=IR
V1=IR1,V2=IR2,V3=IR3
∵V=V1+V2+V3 ∴ IR=IR1+IR2+IR3
⇒IR=I(R1+R2+R3) ∴ R=R1+R2+R3
Now , R1=6Ω R2=9Ω R3=18Ω
In parallel combination
1R=1R1+1R2+1R3 ⇒ 1R=16+19+118=3+2+118=618=13
∴1R=13 ⇒ R=3Ω
Similar Questions
Establish a relationship to determine the equivalent resistance R of a combination of three resistors having resistances R1,R2andR3 connected in series.
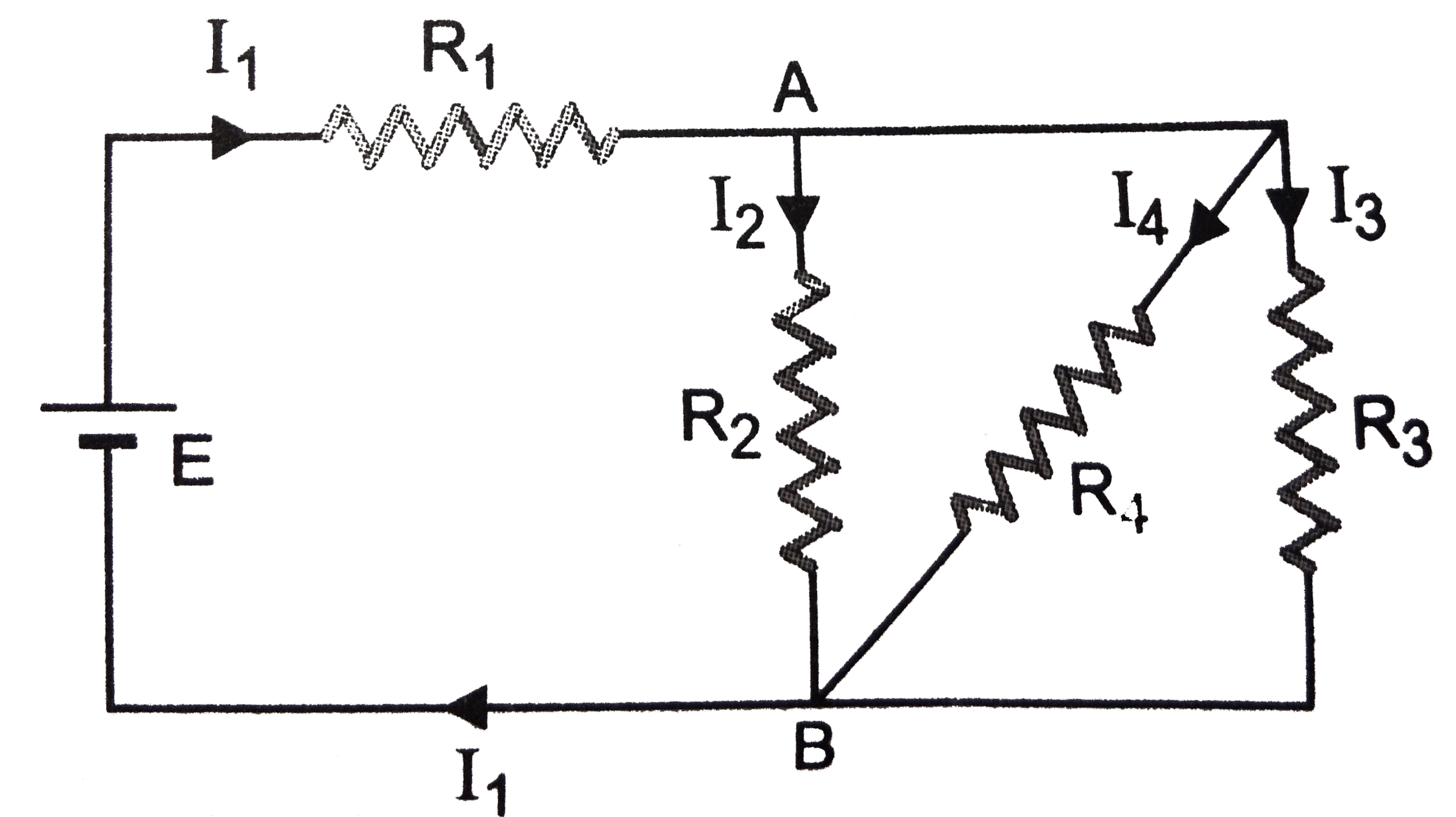
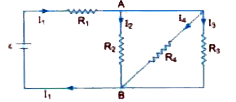
(b) Calculate the equivalent resistance R of a combination of three resistors of 2Ω,3Ωand6Ω joined in parallel.View SolutionIn the circuit R1=4Ω,R2=R3=15ΩR4=30ΩandE=10V Calculate the equivalent resistance of the circuit and current in each resistor
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Equivalent resistance R, of the parallel combination when two resistors Rand R, are connected in parallel is equal to
ARp=R1+R2R1R2BRp=R1R2R1−R2CRp=R1−R2R1+R2DRp=R1+R2R1+R2 - Question 2 - Select One
The correct combination of three resistances 1Ω,2Ωand3Ω to get equivalent resistance 115Ω is
AAll three are combines in paralleBAll three are combines in paralleC1Ωand2Ω in parallel and 3Ω is in series to bothD2Ωand3Ω in parallel and 1Ω is in series to both - Question 3 - Select One
Three identical resistors, each of 6Ω are connected in parallel. The equivalent resistance of the combination will be ______.
A6ΩB18ΩC2ΩD3Ω
Show how would you join three resistors, each of resistance 9Ω so that the equivalent resistance of the combination is (i) 13.5Ω , (ii) 6Ω ?
View SolutionShow how would you join three resistors, each of resistance 9Ω so that the equivalent resistance of the combination is (i) 13.5Ω(ii)6Ω?
View SolutionIn the circuit shown , R1=4Ω,R2=R3=15Ω,R4=30Ω and ε=10V . Calculate the equivalent resistance of the circuit and the current in each resistor.
 View Solution
View SolutionA 5Ω resistor is connected in series with a parallel combination of n resistors of 6Ω each. The equivalent resistance is 7Ω. Find n
View SolutionA parallel combination of three resistors takes a current of 5 A from a 20 V supply. If the resistors are of 10Ωand8Ω find the value of the third resistor.
View Solution

