(a) With the help of a suitable circuit diagram peove that the reciprocal of the equivalent
resistance of a group of resistances joined in parallel is equal to the sym of the
reciprocals of the individual resistances.
(b) In an electric circuit two resistors of 12Ω each are joined in parallel to a 6V battery.
Find the current drawn from the battery.
(a) Connect 3 resistors R1,R2 and R3 in parallel between the
point XY with a battery, a plug key and an ammeter in
series as shown in the figure.
⋅Connect the voltmeter in parallel with these resistors
between the terminals X and Y.
⋅ Plug the key and note the current I in the ammeter and
Potential difference VB across the resistors.
⋅ Take out the plug from the key. Remove the ammeter and voltmeter from the circuit.
Insert the ammeter in series with the resistor R1. Let the ammeter reading be I1.

Similarly measure the currents through R2 and R3. Let these be I2 and I3 respectively.
It is observed that the total current I is equal to the sum of the separate currents through
each branch of the combination.
I=I1+I2+I3
Let RP be the equivalent resistance of the parallel combination of resistors. By applying
Ohm's law to the parallel combination of resistors, we have I=VRP.
On applying Ohm's law to each resistor, we get
I1=VR1, I2=VR2, I3=VR3
Hence VRP=VR1+VR2+VR3or1RP=1R1+1R2+1R3
Thus, the reciprocal of the equivalent resistance of a group of resistances joined in
parallel is equal to the sum of the reciprocals of the individual resistances.
(b) 1Req=1R1+1R2=112+112=212
Req=6Ω ∴I=VReq=66=1A
Topper's Solved these Questions
- BOOK - X BOARDSCHAPTER - X BOARDSEXERCISE - SET-I SECTION-E4videos
X BOARDS
- BOOK - X BOARDSCHAPTER - X BOARDSEXERCISE - SET-II SECTION-A1videos
X BOARDS
- BOOK - X BOARDSCHAPTER - X BOARDSEXERCISE - SET-I SECTION-C3videos
X BOARDS
- BOOK - X BOARDSCHAPTER - SAMPLE QUESTION PAPER EXERCISE - Section-B11videos
SAMPLE QUESTION PAPER
Similar Questions
(a) With the help of a circuit diagram, obtain the relation for the equivalent resistance of two resistances connected in parallel.
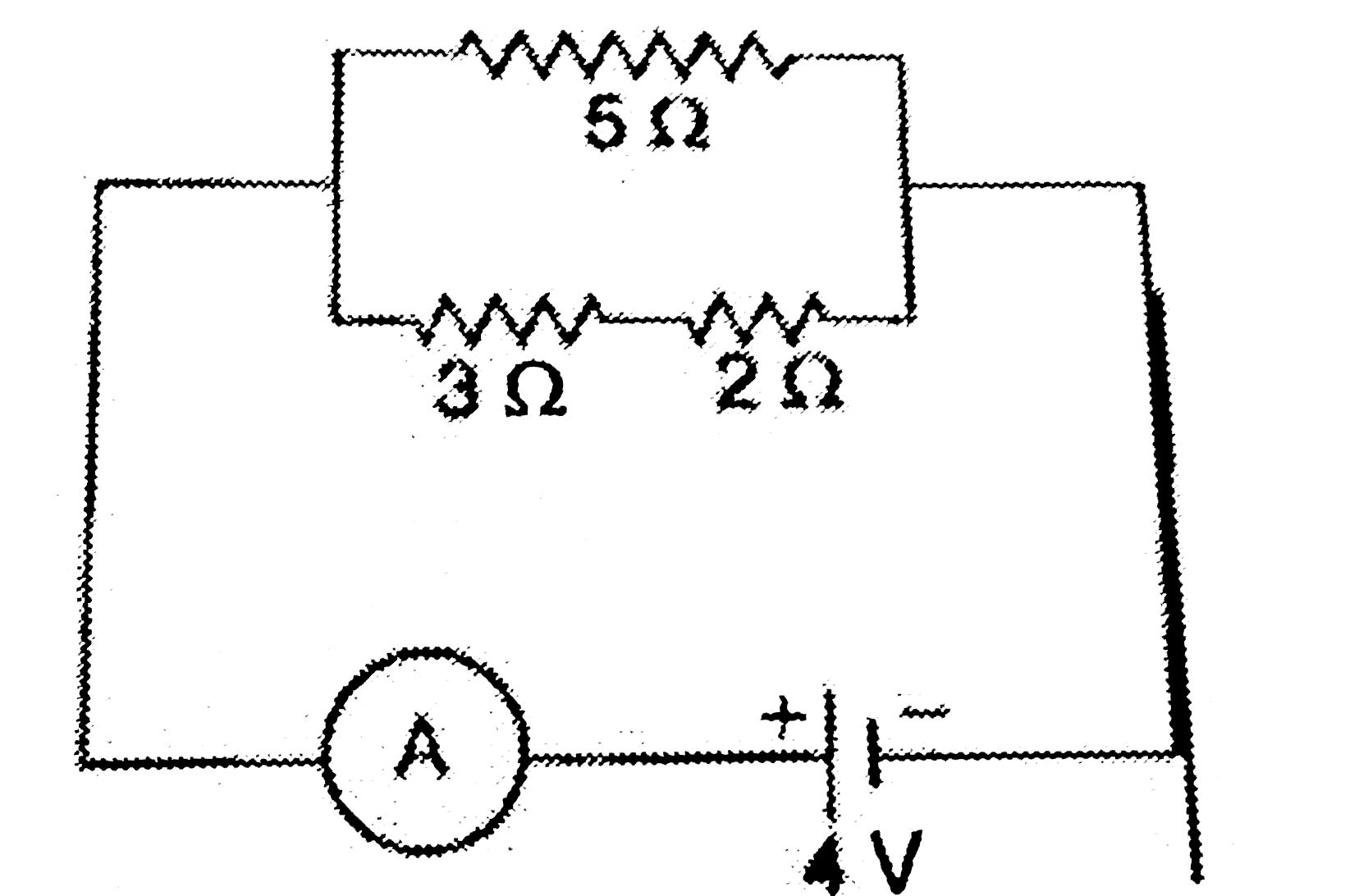
(b) In the circuit diagram shown below, find:
(i) Total resistance.
(ii) Current shown by the ammeter A
 View Solution
View SolutionFind an expression for equivalent resistance of three resistors joined in parallel.
View Solution
Knowledge Check
- Question 1 - Select One
In the circuit shown, if the 10Ω resistance is replaced by 20Ω then what is the amount of current drawn from the battery ?
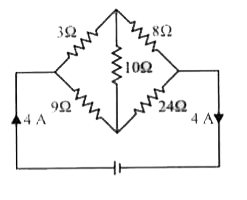 A10AB4AC8AD2A
A10AB4AC8AD2A - Question 2 - Select One
Three resistances, each of1Ω are joined in parallel. Three such combinations are put in series. The equivalent resistance is given by
A9ΩB1ΩC3ΩD13Ω
A wire having a resistance of 18Ω is cut into three equal parts. What is the equivalent resistance if these three parts are joined in parallel ?
View SolutionA wire of 15 Ω resistance is gradually stretched to double its original length. It is then cut into two equal parts. These parts are then connected in parallel across a 3.0 volt battery. Find the current drawn from the battery.
View SolutionA wire of 20Ω resistance is gradually stretched to double its original length. It is then cut into two equal parts. These parts are then connected in parallel across a 4.0 volt battery. Find the current drawn from the battery.
View SolutionEach resistance is of 1Ω in the circuit diagram shown in figure. Find out equivalent resistance between A and B.
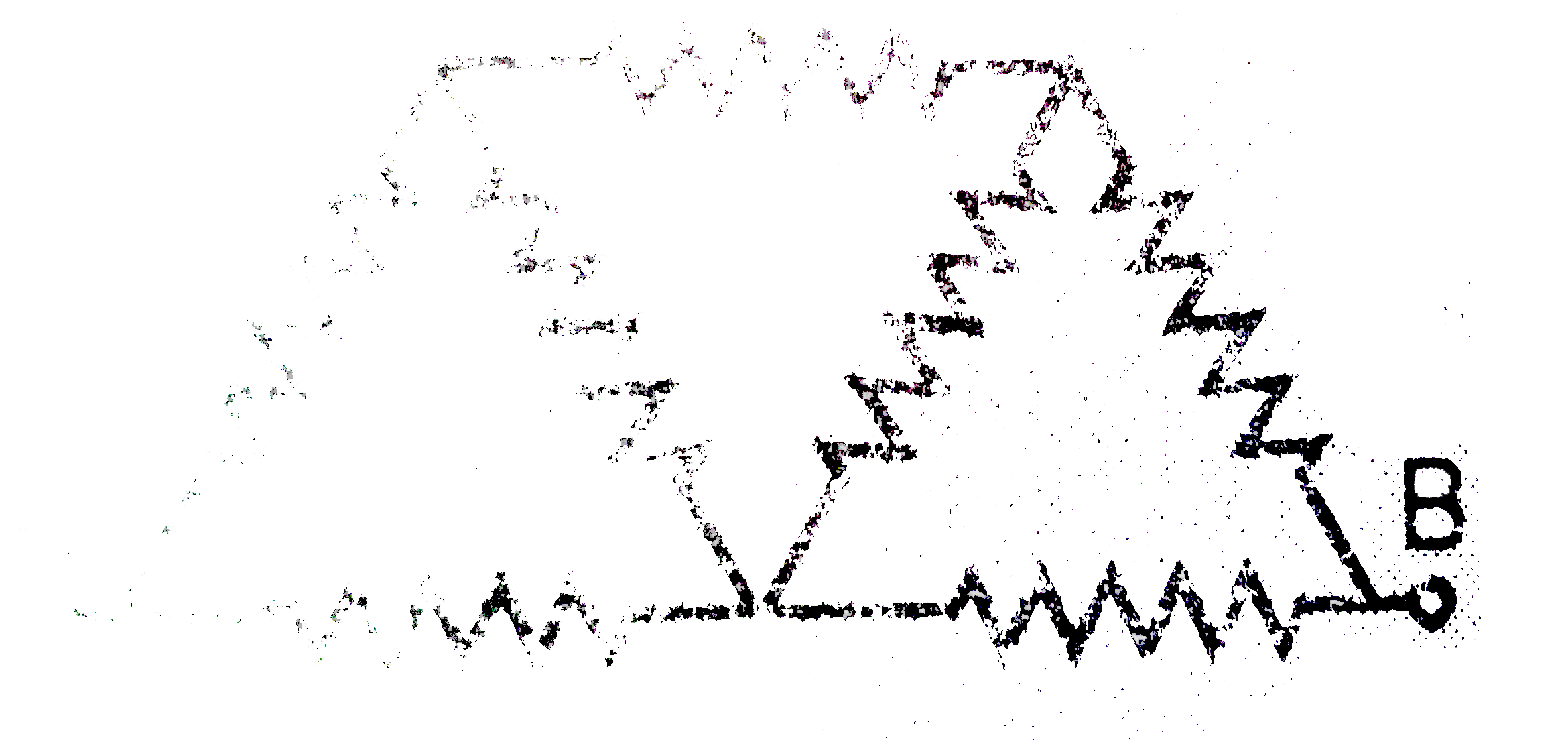 View Solution
View SolutionA battery of emf 6V internal resistance 5Ω is joined in parallel with another cell of emf of 10V and internal resistance 1Ω and the combination is used to send current through a resistor of 12Ω. Calculate the current through each battery.
View SolutionEach resistor shown in figure has a resistance of 10(Ω)and the battery has an emf of 6 V.Find the current supplied by the battery .
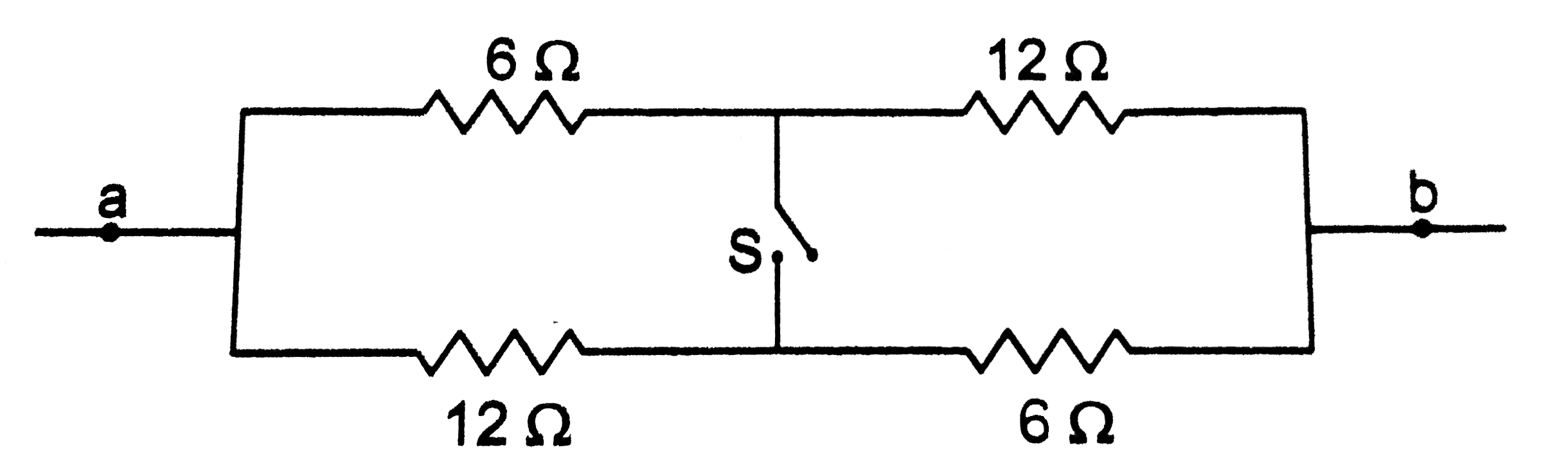 View Solution
View Solution

