While stud dying the dependence of potential difference (V) across a resistor on the current
(I) passing through it, in order to determine the resistance of the resistor, a student took
5 readings for different values of current and plotted a graph between V and I. He got a
straight line graph passing through the origin. What does the straight line signify? Write
the method of determining resistance of the resistor using this graph.
To solve the problem, we need to analyze the relationship between potential difference (V) and current (I) in a resistor, and how to determine the resistance from the graph plotted between these two quantities.
1. Understanding the Graph:
- The student plotted a graph of potential difference (V) on the y-axis and current (I) on the x-axis.
- The resulting graph is a straight line that passes through the origin (0,0).
2. Significance of the Straight Line:
- A straight line graph indicates that there is a linear relationship between V and I.
- According to Ohm's Law, this relationship can be expressed as V=I×R, where R is the resistance.
- Since the graph is a straight line through the origin, it signifies that the resistance (R) is constant for the resistor.
3. Determining Resistance from the Graph:
- The slope of the straight line in the V-I graph represents the resistance of the resistor.
- The slope (m) can be calculated using the formula:
m=ΔVΔI
- Here, ΔV is the change in potential difference and ΔI is the change in current.
4. Calculating Resistance:
- From the slope, we can express resistance as:
R=VI
- Therefore, to find the resistance of the resistor, one can take any point on the straight line, where you have values of V and I, and calculate:
R=VI
5. Conclusion:
- The resistance of the resistor can be determined by calculating the slope of the straight line on the V-I graph, which is equal to the ratio of potential difference to current.
- The student plotted a graph of potential difference (V) on the y-axis and current (I) on the x-axis.
- The resulting graph is a straight line that passes through the origin (0,0).
- A straight line graph indicates that there is a linear relationship between V and I.
- According to Ohm's Law, this relationship can be expressed as V=I×R, where R is the resistance.
- Since the graph is a straight line through the origin, it signifies that the resistance (R) is constant for the resistor.
- The slope of the straight line in the V-I graph represents the resistance of the resistor.
- The slope (m) can be calculated using the formula:
m=ΔVΔI
- Here, ΔV is the change in potential difference and ΔI is the change in current.
- From the slope, we can express resistance as:
R=VI
- Therefore, to find the resistance of the resistor, one can take any point on the straight line, where you have values of V and I, and calculate:
R=VI
- The resistance of the resistor can be determined by calculating the slope of the straight line on the V-I graph, which is equal to the ratio of potential difference to current.
Topper's Solved these Questions
- BOOK - X BOARDSCHAPTER - X BOARDSEXERCISE - SET-II SECTION-A1videos
X BOARDS
- BOOK - X BOARDSCHAPTER - X BOARDSEXERCISE - SET-II SECTION-C1videos
X BOARDS
- BOOK - X BOARDSCHAPTER - X BOARDSEXERCISE - SET-I SECTION-D5videos
X BOARDS
- BOOK - X BOARDSCHAPTER - SAMPLE QUESTION PAPER EXERCISE - Section-B11videos
SAMPLE QUESTION PAPER
Similar Questions
Knowledge Check
- Question 1 - Select One
Equation of straight line passing through origin
AY=mx,BY=CCX= myDX=C - Question 2 - Select One
To study the dependence of current (I) on the potential difference (V) across a resistor, the correct way of connecting the ammeter and voltmeter in the circuit is :
Aammeter and voltmeter both are connected in seriesBammeter is connected in parallel and voltmeter in seriesCammeter is connected in series and voltmeter in parallelDammeter and voltmeter both are connected in parallel - Question 3 - Select One
Which of the following straight lines passes through the origin?
Ax + y = 4Bx2+y2=−6Cx + y =5Dx =4y
In an experiment to study the dependence of current on potential difference across a resistor, a student obtained the graph as shown in the diagram.
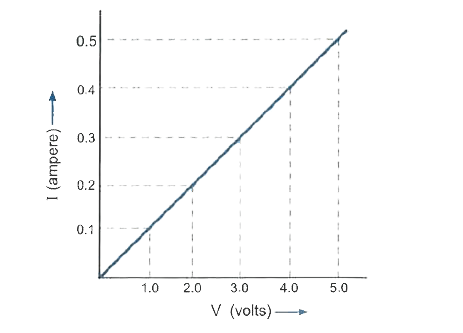
Find the value of resistance of the resistor?View SolutionThe graph between V and I for a conductor is a straight line passing through the origin.
(a) Which law is illustrated by such a grph?
(b) What should remain constant in a statement of this law?View SolutionA 6-V battery is connected across a 5−Ω resistor.Calculate the current passing through the resistor .
View SolutionWhen a potential difference is applied across, the current passing through
View SolutionIn an electric circuit, potential difference across a lamp is 20 V and current through the lamp is 0.5A. The resistance of the lamp is
View Solution

