BCDE is a parallelogram. O is a point inside BCDE. OB, OC, OD and OE are joined. Prove that triangle BOC + triangle EOD = triangle EOB + triangle DOC.
Step by step video & image solution for BCDE is a parallelogram. O is a point inside BCDE. OB, OC, OD and OE are joined. Prove that triangle BOC + triangle EOD = triangle EOB + triangle DOC. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023সম্পর্কিত প্রশ্ন
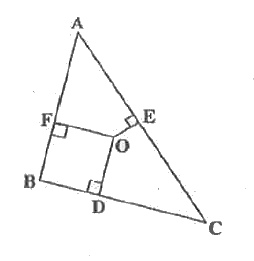
In Fig. 2.54, o is a point in the interior of a triangle ABC,OD⊥BC,OE⊥ACandof⊥AB. Show that
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2,
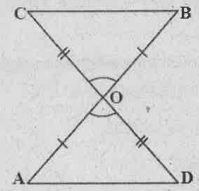
View Solutionఇచ్చిన పటంలో AB మరియు CD లు 'O' వద్ద ఖండించుకొనుచున్నాయి. OA=OB మరియు OD=OC అయిన ΔAOD=ΔBOC
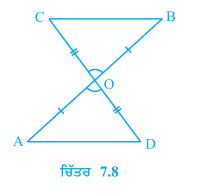
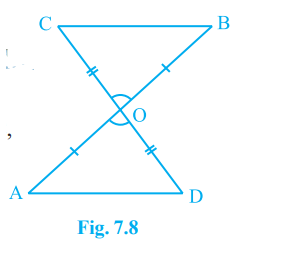
View Solutionਚਿੱਤਰ 7.8 ਵਿੱਚ OA = OB ਅਤੇ OD = OC ਹੈ ਸਿਧ ਕਰੋ (i) ΔAOD≅ΔBOC ਅਤੇ (ii) AD || BC.
View SolutionO is any point in the interior of a triangle ABC.
Prove that :
OB+OC<AB+AC.
 _Q01.png" width="60%">
_Q01.png" width="60%">
View SolutionIn Fig. 7.8, OA = OB and OD = OC. Show that (i) ΔAOD≅ΔBOC and (ii) AD || BC.
View SolutionO' is an interior point of a parallelogram ABCD. Prove that :
area of ΔAOB+ area of ΔCOD= area of ΔAOD+ area of ΔBOC
View SolutionIn the figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that ar( Delta DOC) = ar( Delta AOB)
View SolutionFind the perimeter of the given figure : BCDE is a square and ABC is an equilateral triangle.

View Solution
