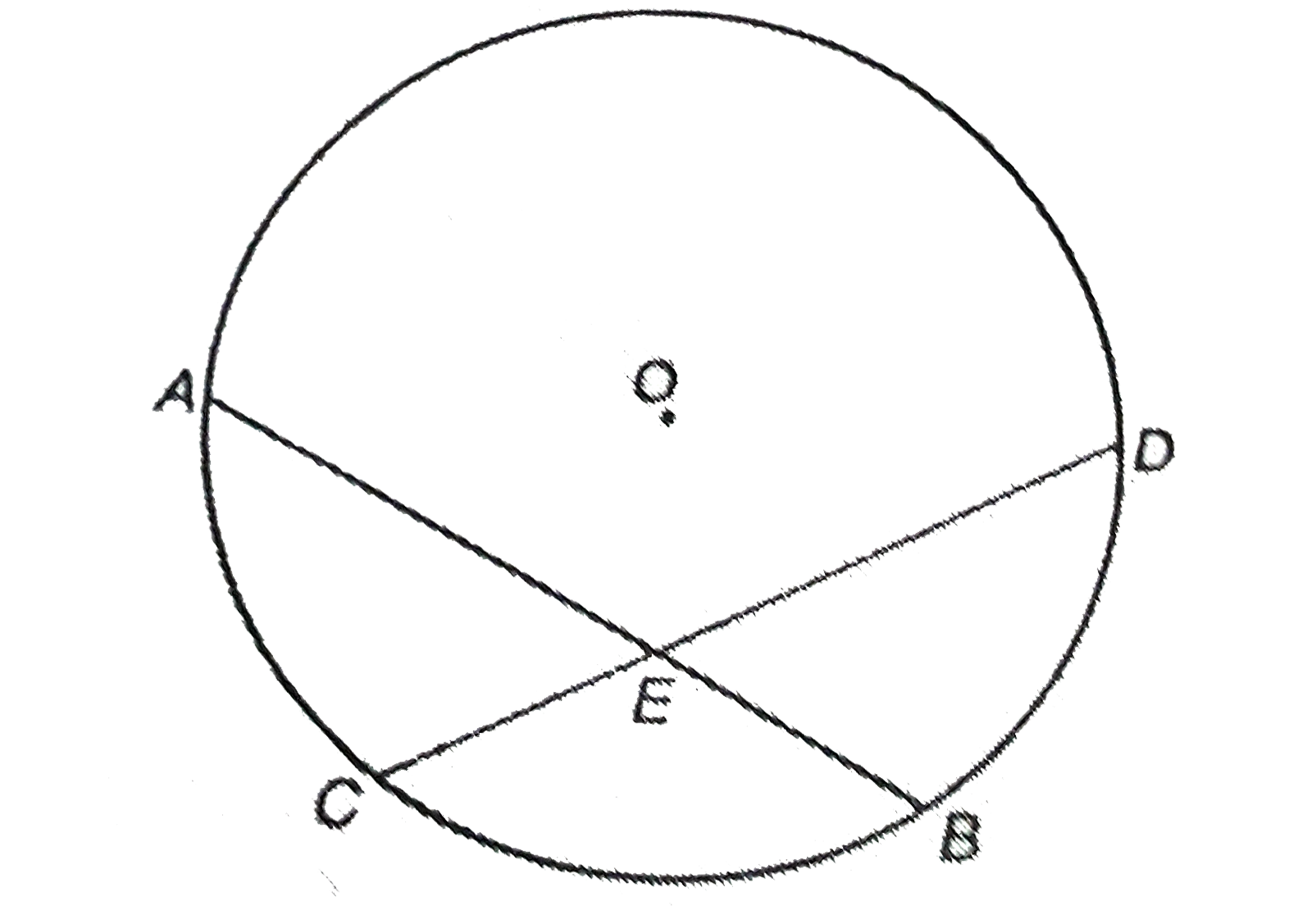
In the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
CF=CG
∠CFEand∠CGE
∠CFE=∠CGE=90o
CE=CF
CF=CG
∠CFE≅∠CGE
so,FE=EG
Similarly,AF=DG
AF+FE=DG+GT
AE=DE
so,EB=EC
∠AECand∠DEB is similar
ACBD=AEDE=CEBE=1
So, AC=BD
Similar Questions
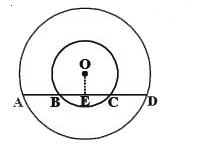
In the adjacent figure, there are two concentric circles with centre ‘O’. Chord AD of the bigger circle intersects the smaller circle at B and C. Show that AB = CD.
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn this figure AB and CD intersect each other at E in such a way that DE=BE And EA=EC Prove that AD=CB
View SolutionChords AB and CD of a circle with centre O, intersect at a point E. If OE bisects angle AED, prove that chord AB = chord CD.
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.
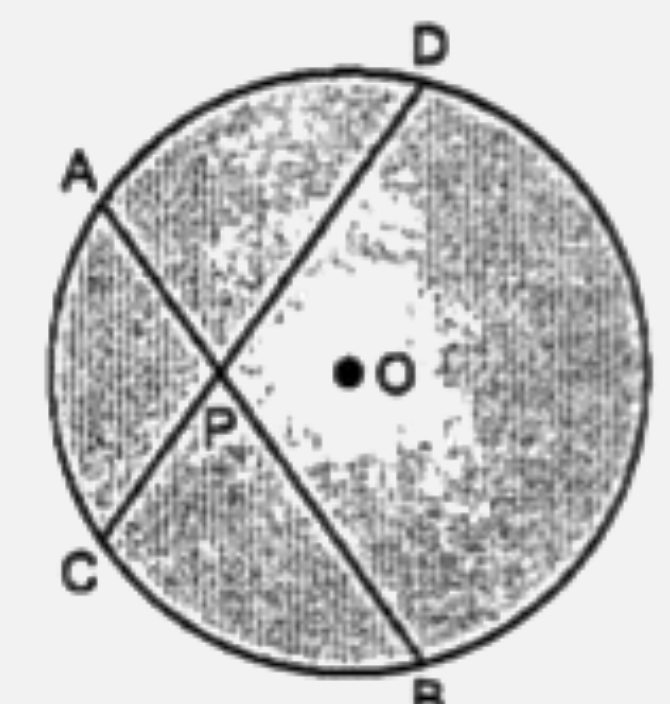
Prove that:
BP=DP
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.
View SolutionTwo chords AB, CD of a circle with centre O intersect each other at P. ∠ADP=23∘ and ∠APC=70∘, then the ∠BCD is
View SolutionTwo chords AB and CD of circle having centre O intersect each other at P. If ∠APC=40∘, then ∠AOC+∠BOD=
View Solution
