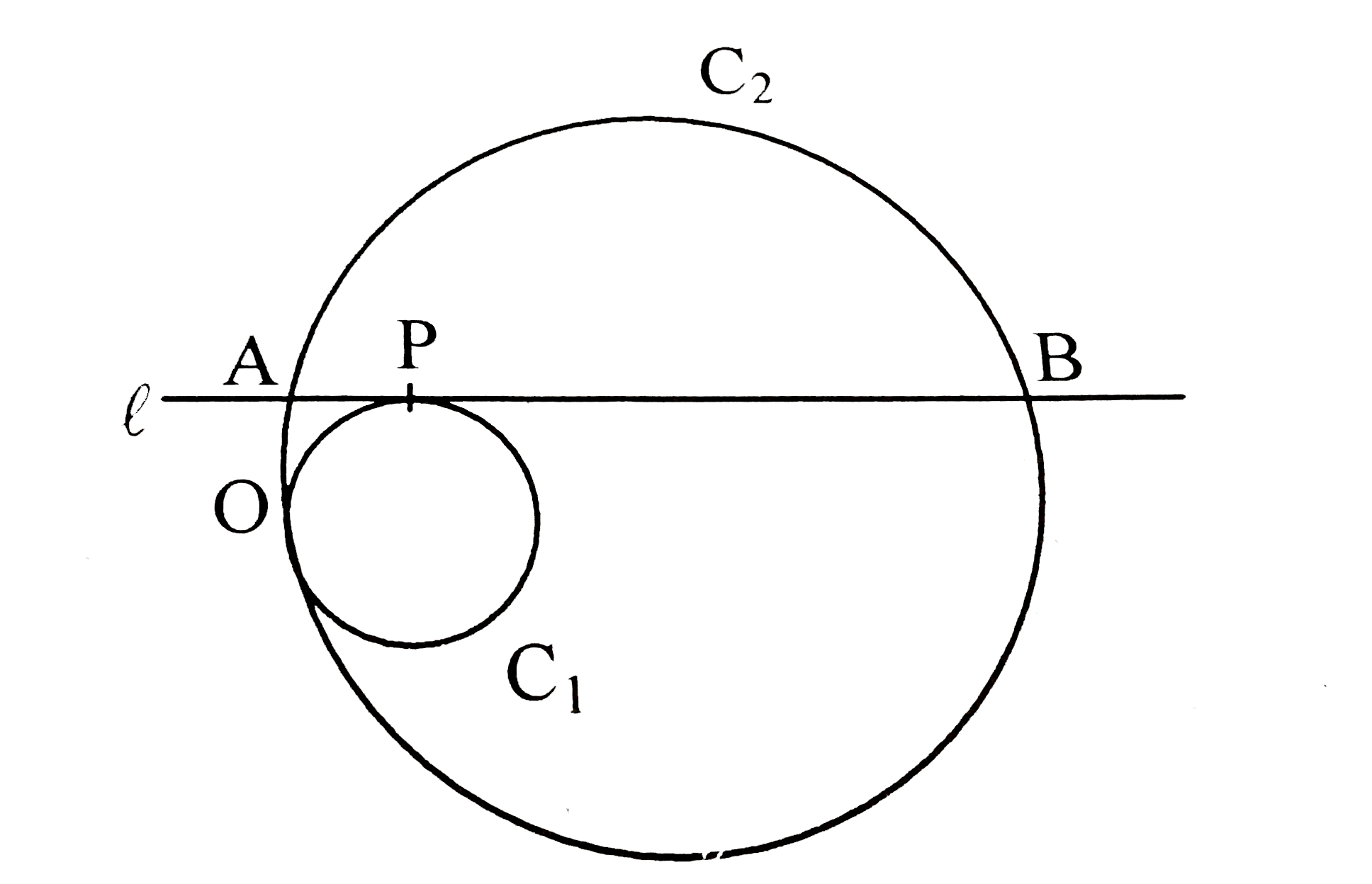
The centres of two circles C1 and C2, each of unit radius are at a distance of 6 units from each other. Let P be the mid point of the line segment joining the centres of C1 and C2, and C be a circle touching circles C1 and C2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C. then the radius of the circle C is.
∠O'PQ=α=∠RPO
(vartical opposite angle)
∠CPR=900−α
O'Q=1
PO'=3
PQ=√PO'2−O'Q2
PQ=√9−1=√8=2√2
∠PO'Q
cosα=2√23
sinα=13
tanα=12√2
In∠PIK
tanα=2√2r
12√2=2√2r
r=8unit
Similar Questions
The centres of two circles C1 and C2 each of unit radius are at a distance of 6 units from each other. Let P be the mid point of the line segment joining the centres of C1 and C2 and C be a circle touching circles C1 and C2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C is
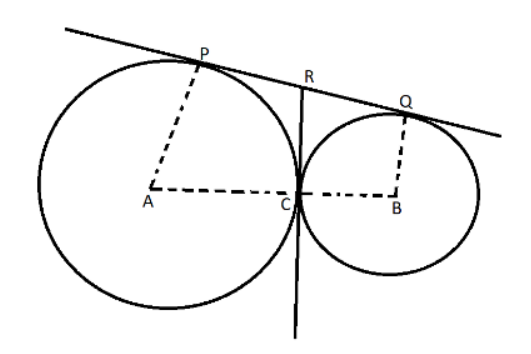
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View Solution
Knowledge Check
The centres of two C1 and C2, each unit of unit radii, are at a distance of 6 units from each other. Let P be the mid-point of the line segment joining the centres of C1andC2. A third circle C is drawn such that it is externally tangent to both the circles C1andC2 at the same points where the lines passing through P are tangent to the circles C1andC2. The radius of the circle C is
A8B6C6√2D4√2Let C be the circle with centre (1,1) and radius 1 . If T is the circle centred at (0,y) , passing through origin and touching the circle C externally , then the radius of T is equal to
A12B14C√3√2D√32Circles C1 and C2 of radii r and R respectively, touch each other as shown in the figure. The lime l, which is parallel to the line joining the centres of C2 and C2 is tangent to C1 at P and intersects C2 at A,B.If R2=2r2, then ∠AOB equals-
 A2212∘B45∘C60∘D6712∘
A2212∘B45∘C60∘D6712∘
In Fig. 10.21, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q . (FIGURE)
View SolutionLet C be the circle with centre at (1, 1) and radius = 1. If T is the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to (1) √3√2 (2) √32 (3) 12 (3) 14
View SolutionC1 and C2 are circle of unit radius with centers at (0, 0) and (1, 0), respectively, C3 is a circle of unit radius. It passes through the centers of the circles C1andC2 and has its center above the x-axis. Find the equation of the common tangent to C1andC3 which does not pass through C2.
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
View SolutionThe circle C has its centre at (−1,1) and touches both the coordinate axes. From a point P(2,3) tangents are drawn to touch C at Q and R. The equation of the line joining the midpoints of PQ and PR is
View Solution
