PQRS एक a भुजा का वर्ग है। सिद्ध कीजिए की PQ तथा PS को अक्ष मानकर खींचे गये वर्ग के परिगत वृत्त का समीकरण x2+y2=a(x+y) है।
माना PQ के अनुदिश x-अक्ष तथा PS के अनुदिश y-अक्ष है।
माना परिगत वृत्त का केन्द्र O है, जो वर्ग का भी केन्द्र होगा।
O से PQ पर लम्ब OE डाला, तब
PE=OE=12a
OP को मिलाया, तब समकोण ΔOEP में,
OP2=PE2+OE2=(12a)2+(12a)2=12a2
OP=a√2
वृत्त का केन्द्र =(12a,12a)
तथा त्रिज्या =a√2.
अत: परिगत वृत्त का अभीष्ट समीकरण निम्न है-
(x−12a)2+(y−12a)2=(a√2)2
या x2+y2−ax−ay=0 या x2+y2=a(x+y).
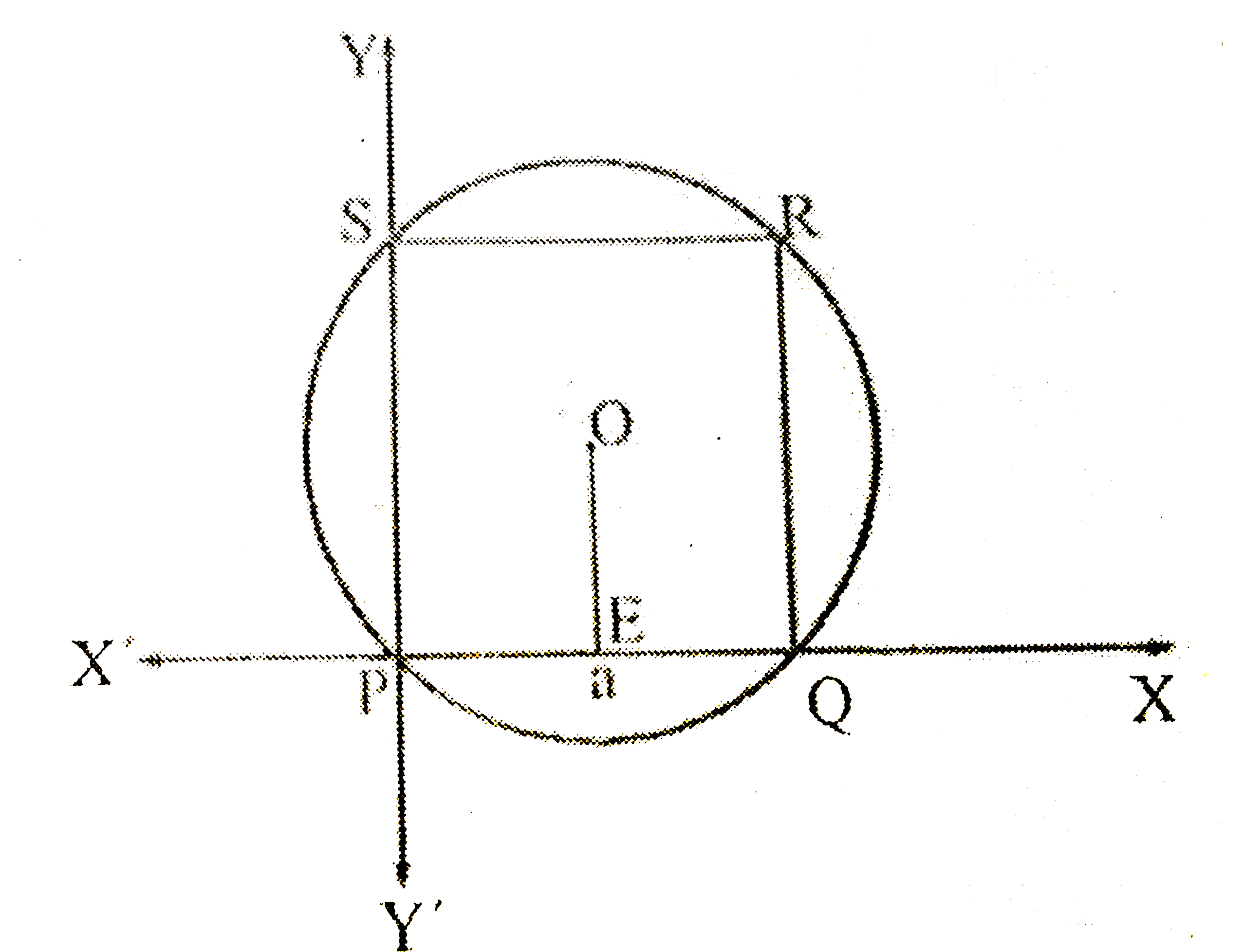
Topper's Solved these Questions
- शंकु परिच्छेद BOOK - MANOHAR RAYCHAPTER - शंकु परिच्छेद EXERCISE - प्रश्नावली 11(A)
16 Videos
- शंकु परिच्छेद BOOK - MANOHAR RAYCHAPTER - शंकु परिच्छेद EXERCISE - प्रश्नावली 11(B)
16 Videos
- रैखिक असमिकाएँBOOK - MANOHAR RAYCHAPTER - रैखिक असमिकाएँEXERCISE - प्रश्नावली 6(D)
19 Videos
- समुच्चयBOOK - MANOHAR RAYCHAPTER - समुच्चयEXERCISE - प्रश्नावली 1(G)
23 Videos
Similar Questions
उस वृत्त का समीकरण ज्ञात कीजिए, जिसका :
केन्द्र (2, 3) तथा त्रिज्या 5 है।
View Solutionउन व्रतों के केन्द्र और त्रिज्याएँ ज्ञात कीजिय, जिनके समीकरण निम्नलिखित हैं-
x2+y2+2gx+2fy+c=0
View Solutionअसमिका 4x+3<6x+7 का हल होगा -
View SolutionALLAHABAD शब्द में आये हुए (A ) स्वरों का (B ) अक्षरों का समुच्चय लिखो
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक अनन्त गुणोत्तर श्रेढी का योग x है तथा श्रेढी के सभी पदों का वर्ग करने पर श्रेढी का योग y है । सिद्ध कीजिए कि श्रेढी का सार्व अनुपात x2−yx2+y है ।
View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionपरवलय y=x2−2x+3 का शीर्ष, नाभि, अक्ष तथा नियता का समीकरण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि y2+2ax+2by+c=0 एक परवलय को निरूपित करता है जिसका अक्ष x-अक्ष के समांतर है। इसका शीर्ष तथा इसके नाभिलम्ब का समीकरण ज्ञात कीजिए।
View Solutionएक परवलय के नाभिलम्ब का समीकरण x+y=8 तथा उसके शीर्ष पर स्पर्शी का समीकरण x+y=12 है, तो उसके नाभिलम्ब की लम्बाई है :
View SolutionY - अक्ष के समीकरण का सममित रूप …………. है।
View Solutionवृत्त x2+y2=4 के बिंदु (√3,1) पर खींची गई स्पर्श रेखा और अभिलम्ब तथा X-अक्ष एक त्रिभुज बनाते है । इस त्रिभुज का (वर्ग इकाइयो में) क्षेत्रफल है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solution
