यदि 18∑i=1(xi−8)=9 तथा 18∑i=1(xi−8)2=45हो, तो x1,x2,........x18 का मानक विचलन है -
49
94
32
इनमें से कोई नहीं
The correct Answer is:B, C
माना di−xi−8, परन्तु
σ2x=σ2d=118∑d2i−(118∑di)2=118×45−(918)2=94
∴σx=32.
Topper's Solved these Questions
- BOOK - MANOHAR RAYCHAPTER - सांख्यिकीEXERCISE - विभिन्न इंजीनियरिंग परीक्षाओं के हल सहित प्रश्न6videos
सांख्यिकी
- BOOK - MANOHAR RAYCHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 15(C)8videos
सांख्यिकी
- BOOK - MANOHAR RAYCHAPTER - सरल रेखाएँEXERCISE - प्रश्नावली 10(D)28videos
सरल रेखाएँ
- BOOK - MANOHAR RAYCHAPTER - सीमा और अवकलन EXERCISE - प्रश्नावली 13(C)13videos
सीमा और अवकलन
Similar Questions
एक कक्षा के सभी विधार्थियों ने गणित में कम अंक प्राप्त किये । अध्यापक ने प्रत्येक विधार्थी को 10 रियायती अंक देने का निर्णय लिया । रियायती अंक देने के बाद भी निम्नलिखित में से कौन - सी सांख्यिकी माप नहीं बदलेगी ?
03:57View Solutionनिम्नलिखित सारणी एक विधालय के 50 छात्रों की उपस्थिति को दर्शाता है । दिए गए आँकड़ों से माध्य , मानक विचलन तथा विचरण गुणांक की गणना कीजिए ।
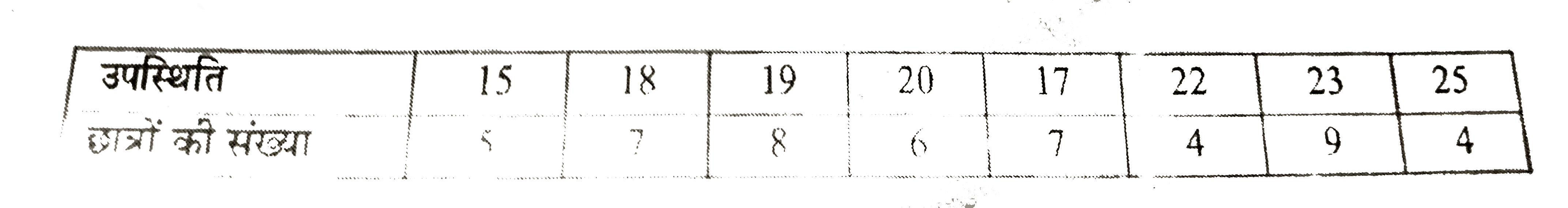 02:26View Solution
02:26View Solution(1 ,2 ) तथा (3 ,7 ) बिन्दुओ से जाने वाली रेखा की ढाल है -
02:41View Solutionनिम्न फलनों के x साक्षेप अवकल - गुणांक प्रथम सिद्धांत से ज्ञात कीजिए :
(i) x3 (ii) −x
(iii) (−x)−1 (iv) √3
(v) 1x2 (vi) x3−27 (vii) (x−1)(x−2) (viii) x+1x−106:25View SolutionSTATEMENT-1: If sum_(i=1)^(9)(x_(i)-8)=9 and sum_(i=1)^(9)(x_(i)-8)^(2)=45 then s.D.~ of~ x_(1),x_(2),.....,x_(9), is 2. STATEMENT- 2: S.D.is independent of change of origin.
03:52View SolutionIf sum_(i=1)^(10)(x_(i)-15)=12 and sum_(i=1)^(10)(x-15)^(2)=18 then the S.D.of observation x_(1),x_(2),x_(3),....x_(10) is:
03:28View SolutionIf 9∑i=1(xi−5)=9and9∑i=1(xi−5)2=45 then the standard deviation of the 9 items x1,x2,.....,x9 is
03:24View SolutionIf 7∑i=1i2xi=1 and 7∑i=1(i+1)2xi=12 and 7∑i=1(i+2)2xi=123 then find the value of 7∑i=1(i+3)2xi____
02:14View SolutionIf x1,x2,"…......." x18 are observation such that 18∑j=1(xj−8)=9 and 18∑j=1(xj−8)2=45, then the standard deviation of these observations is
01:53View Solutionयदि 9∑i=1(xi−5)=9 तथा 9∑i=1(xi−5)2=45 है, तब 9 अवयवों x1,x2,…,x9 का मानक विचलन है
View SolutionThe standard deviation of n observations x1,x2,......,xn is 2. If n∑i=1xi=20 and n∑i=1x2i=100 then n is
View SolutionIf 9∑i=1(xi−5)=9and9∑i=1(xi−5)2=45, then the standard deviation of the 9 items x1,x2,......,x9 is
01:41View SolutionIf 18∑i=1(xi−8)=9 and 18∑i=1(xi−8)2=45 then the standard deviation of x1,x2,...,x18 is
04:15View SolutionIf 18∑i=1(xi−8)=9 and 18∑i=1(xi−8)2=45 then find the standard deviation of x1,x2,….x18
06:17View SolutionIf 18∑i=1(xi−8)=9 and 18∑i=1(xi−8)2=45 then the standard deviation of x1,x2,…,x18 is
03:16View Solution
