किसी समान्तर चतुर्भुज ABCD का विकर्ण BD , रेखा AE को बिन्दु F पर प्रतिच्छेदित करता है , जहाँ बिन्दु E , भुजा BC पर स्थित है , तो सिद्ध कीजिए कि DF×EF=FB×FA.
Step by step video, text & image solution for किसी समान्तर चतुर्भुज ABCD का विकर्ण BD , रेखा AE को बिन्दु F पर प्रतिच्छेदित करता है , जहाँ बिन्दु E , भुजा BC पर स्थित है , तो सिद्ध कीजिए कि DFxxEF=FBxxFA. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुज BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6 (C )
2 Videos
- त्रिभुज BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6(C)
16 Videos
- त्रिभुज BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6 (A)
1 Videos
- त्रिकोणमिति के कुछ अनुप्रयोगBOOK - MANOHAR RAYCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोगEXERCISE - लघु उत्तरीय
2 Videos
- दो चार वाले रैखिक समीकरण युग्मBOOK - MANOHAR RAYCHAPTER - दो चार वाले रैखिक समीकरण युग्मEXERCISE - प्रश्नावली 3(I)
20 Videos
Similar Questions
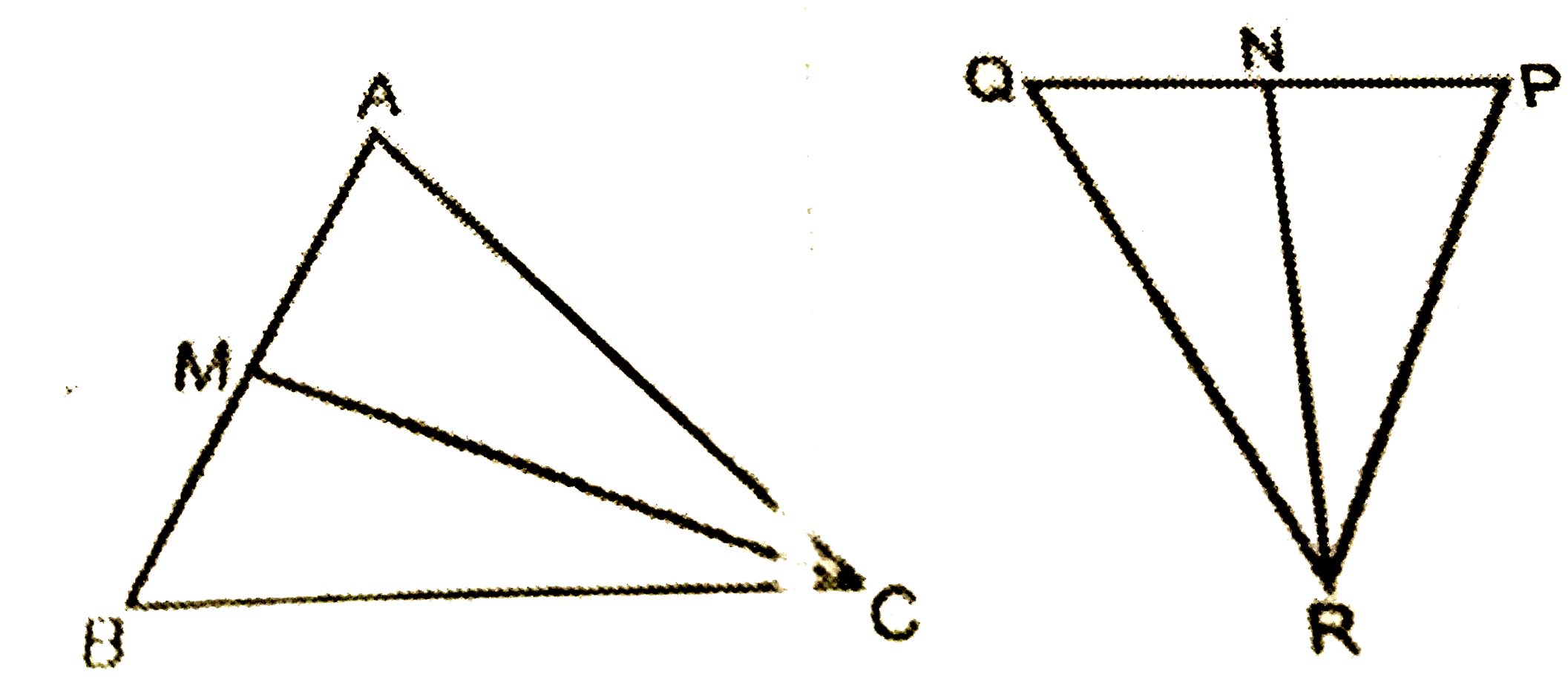
दी हुई आकृति में CM और RN क्रमशः ΔABC और ΔPQR की माध्यिकाएँ हैं । यदि ΔABC~ΔPQR है तो सिद्ध कीजिए :
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQ
(iii) ΔCMC~ΔRNO.
View Solutionनिम्न आकृति में , ΔODC~ΔOBA,∠BOC=125∘ और ∠CDO=70∘ है । ∠DOC,∠DCO और ∠OAB ज्ञात कीजिए ।
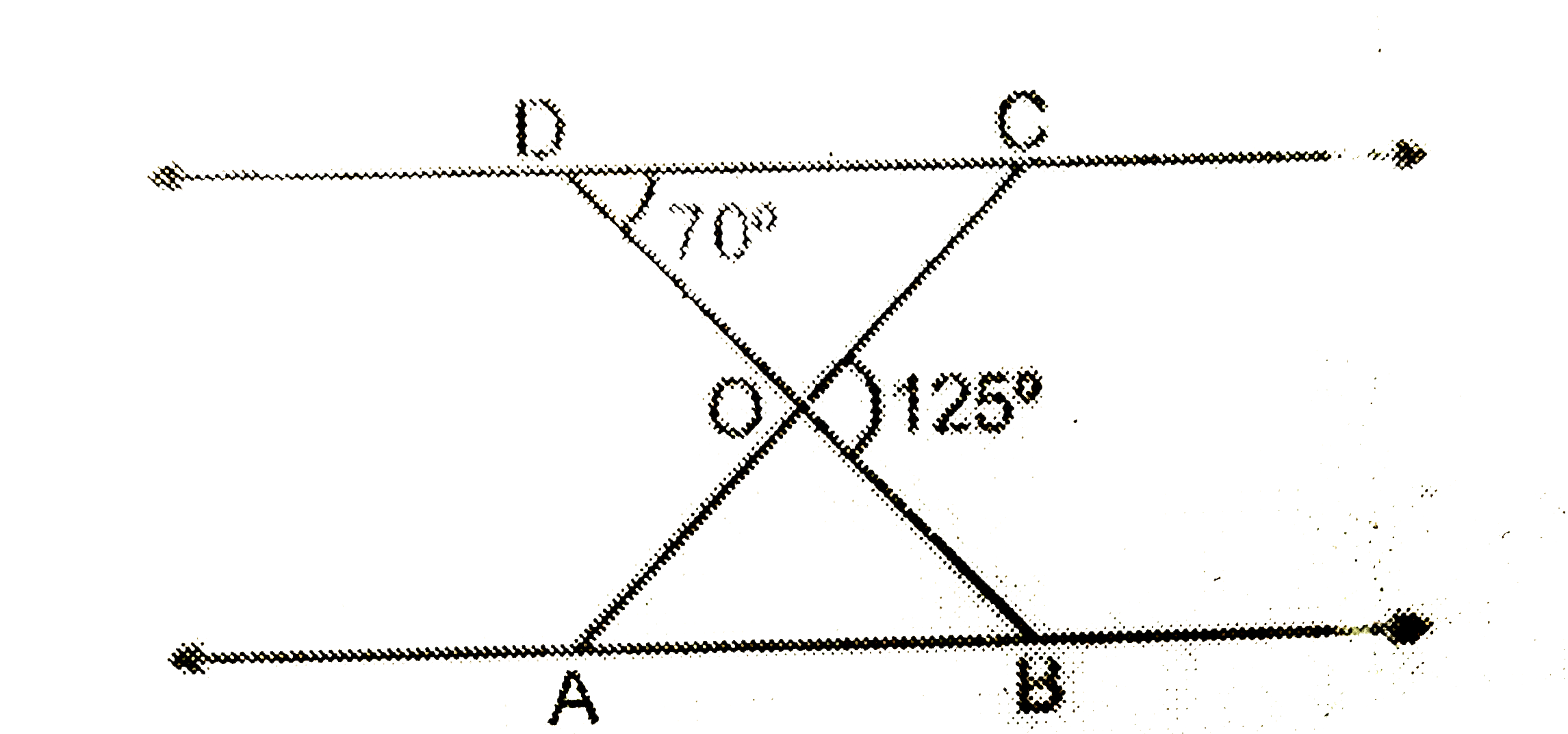
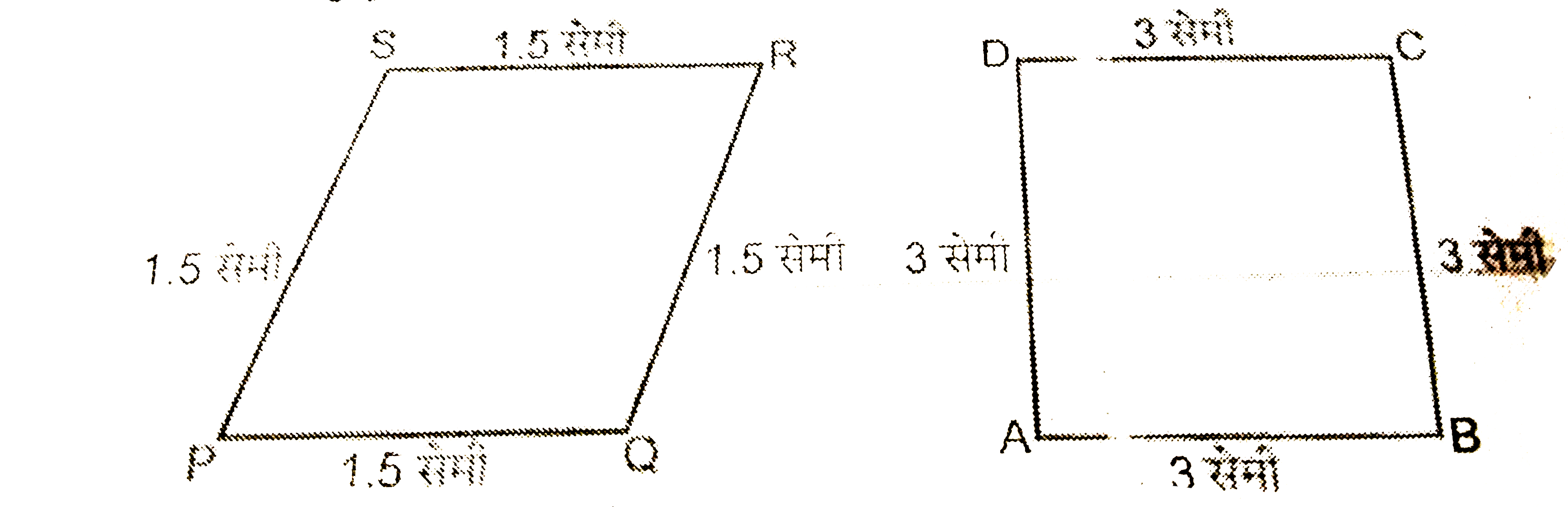
View Solutionबताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं ।
View Solutionएक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधर : खड़ा हैं । टॉवर के ठीक सामने दूसरे के एक अन्य बिंदु से टॉवर शिखर का उन्नयन कोण 60∘ है। इसी तट पर इस बिन्दु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 30∘ है (देखिए आकृति) । टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए ।

View Solutionसमीकरण 8x+5y=11 को संतुष्ट करने वाले बिन्दु के निर्देशांक है :
View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the Side BC. Prove that DF×EF=FB×FA.
View Solutionबिन्दु (1,0,0) से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो XZ-समतल पर लम्ब है।
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
View Solutionकोई फलन किसी बिन्दु x = a पर अवकलनीय कहलता है, जब -
View Solutionकिसी बिन्दु पर संतत फलन होता है -
View Solutionकोई फलन f(x) किसी बिन्दु x2 पर निम्निष्ठ है , तो f''(x2)………..
View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि कोणांक (z) = 0
View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि arg(z−2−3i)=π4
View Solution
