चित्र में, AT वृत्त की बिन्दु A पर स्पर्श रेखा है जहाँ O वृत्त का केन्द्र है। x, y तथा z का मान ज्ञात कीजिए।
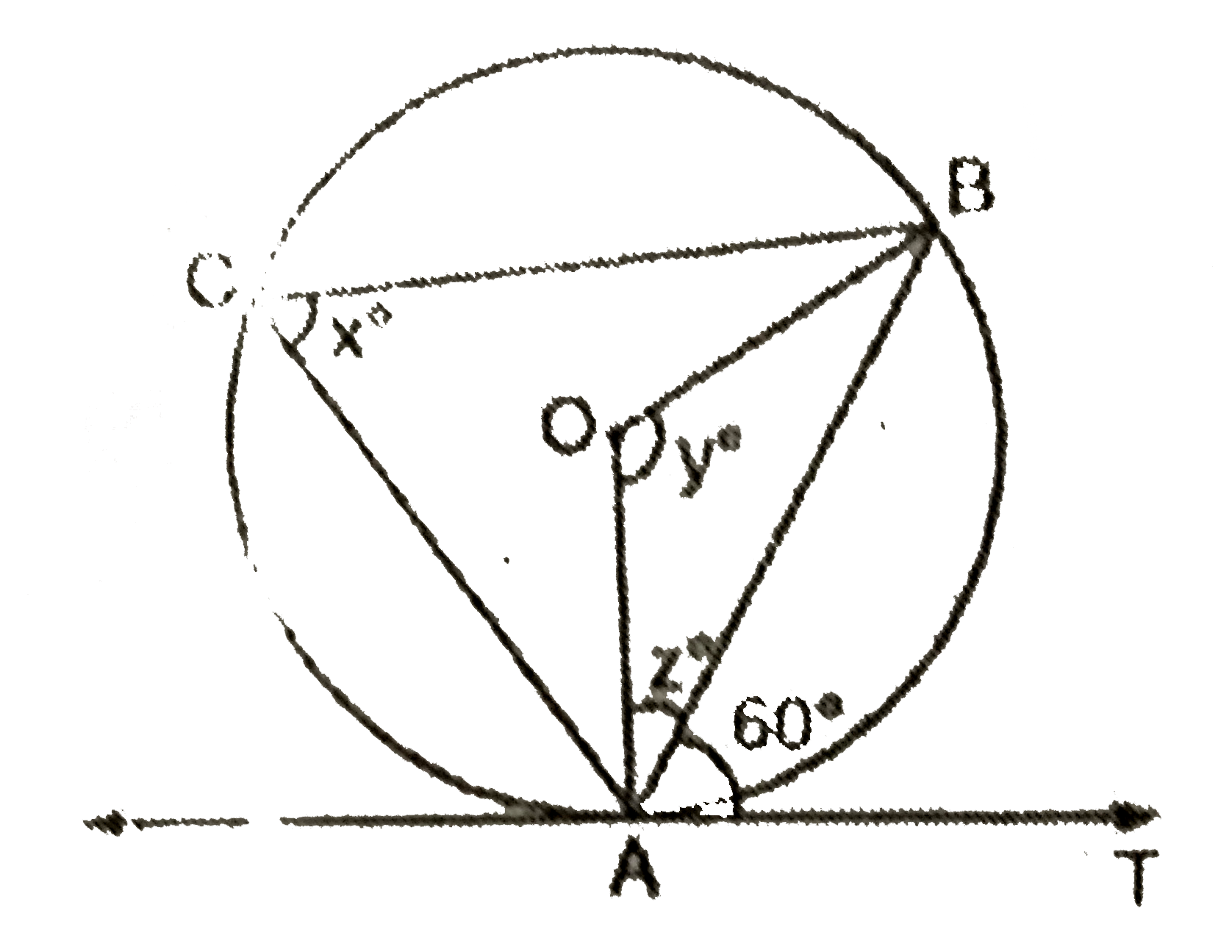
x=60∘ ,y=120∘ ,z=30∘
x=90∘ ,y=120∘ ,z=30∘
x=60∘ ,y=170∘ ,z=30∘
x=60∘ ,y=120∘ ,z=90∘
The correct Answer is:A
∵∠x∘=∠BAT=60∘
तथा ∠AOB=y∘=2∠ACB
y∘=2∠x∘=2×60∘
y∘=120∘
∵∠OAT=60∘+z∘
∴60∘+z∘=90∘
(∵AT एक स्पर्श रेखा है जिस पर बिन्दु O से एक लम्ब रेखा डाली गयी है।)
z∘=90∘−60∘
z∘=30∘
अतः x∘=60∘,y∘=120∘,z∘=30∘

Topper's Solved these Questions
- वृत्तBOOK - MANOHAR RAYCHAPTER - वृत्तEXERCISE - प्रश्नावली 10(A)
4 Videos
- वृत्तBOOK - MANOHAR RAYCHAPTER - वृत्तEXERCISE - प्रश्नावली 10(B)
13 Videos
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(E)
25 Videos
- वृत्तों से संबंधित क्षेत्रफल BOOK - MANOHAR RAYCHAPTER - वृत्तों से संबंधित क्षेत्रफल EXERCISE - प्रश्नावली 12(D)
17 Videos
Similar Questions
रिक्त स्थानो की पूर्ति कीजिए :
(i) किसी वृत्त की स्पर्श रेखा उसे …………… बिन्दु पर प्रतिच्छेद करती है।
(ii) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को …………… कहते है।
(iii) एक वृत्त की …………… समांतर स्पर्श रेखाएँ हो सकती है।
(iv) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ट बिन्दु को ............ कहते है।
View Solutionसिद्ध कीजिए कि स्पर्श बिंदु से स्पर्श रेखा पर खींची गया लम्ब वृत्त के केन्द्र से होकर जाता है।
View Solutionनिन्मलिखित में से परिमेय संख्याएँ छाँटकर लिखिए: √3,π3,2273√4,√414 और 2.33
View Solutionएक वृत्ताकार मार्ग के बाहरी और भीतरी व्यास क्रमश: 8 मीटर और 6 मीटर है। उसके दोनों तरफ तार खींचा जाये तो उसकी लम्बाई होगी :
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
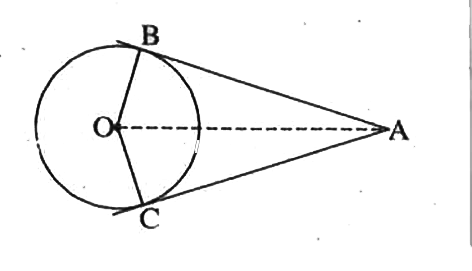
View Solutionदी गई आकृति में AB तथा AC वृत्त की स्पर्श रेखाएं है ,O वृत्त का केंद्र है ,यदि ∠CAB=60∘ तो ∠BOC है -
View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
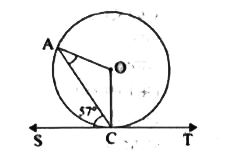
View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
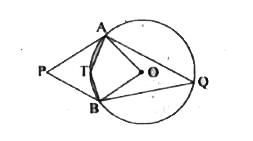
View Solutionआकृति में PQ ,Q केंद्र वाले वृत्त की स्पृह रेखा है जो वृत्त को R पर स्पर्श करती है। यदि कोण TRQ=30∘ हो तो ∠SOR एवं ∠RTO का मान ज्ञात कीजिए।
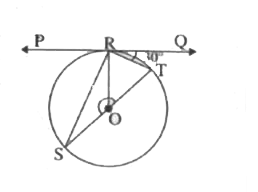
View Solutionउस वृत्त का समीकरण ज्ञात कीजिए जिसका केन्द्र (2,-1) पर हो तथा जो रेखा 3x+4y=12 को स्पर्श करता हो l
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionवृत्त की छेदन रेखा PQ है। छेदन रेखा PQ के स्पर्श रेखा बनने का प्रतिबन्ध किखिये।
View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
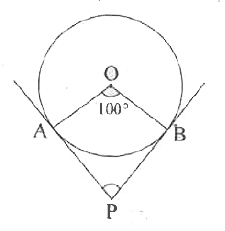
View Solution
