आकृति x>y, में दिखाइएः LM>LN
△MLNमें∠x>∠y
सिद्ध करना है: LM>∠N.
उत्पत्ति ∠1+∠x=180∘ (रैखिकीये युग्म)
∠x=180∘−∠1
तथा ∠2+∠y=180∘ (रैखिकीये युग्म)
∴∠y=180∘−∠2
किन्तु ∠x>∠y (दिया है)
∴180∘−∠1>180∘−∠2
या −∠1<−∠2
या ∠1<∠2
या ∠1<∠2
या LN<LM(∴δ में बड़े कोण के सामबे की भुजा बड़ी होती है)
∴LM>LN.

Topper's Solved these Questions
- त्रिभुजBOOK - MANOHAR RAYCHAPTER - त्रिभुजEXERCISE - प्रशावली7(A)
13 Videos
- त्रिभुजBOOK - MANOHAR RAYCHAPTER - त्रिभुजEXERCISE - प्रश्नावली 7(A)
14 Videos
- चतुर्भुज BOOK - MANOHAR RAYCHAPTER - चतुर्भुज EXERCISE - प्रश्नावली 8(D)
13 Videos
- दो चरों वाले रैखिक समीकरण BOOK - MANOHAR RAYCHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - प्रश्नावली 4.2
1 Videos
Similar Questions
चतुर्बुज ABCD में, AC=AD है और AB कोण A को समद्विभाजित करता है (देखिये आकृति) दर्शाइए की △≅△ABD है BC और BD के बारे में अप्प क्या कहे सकते है
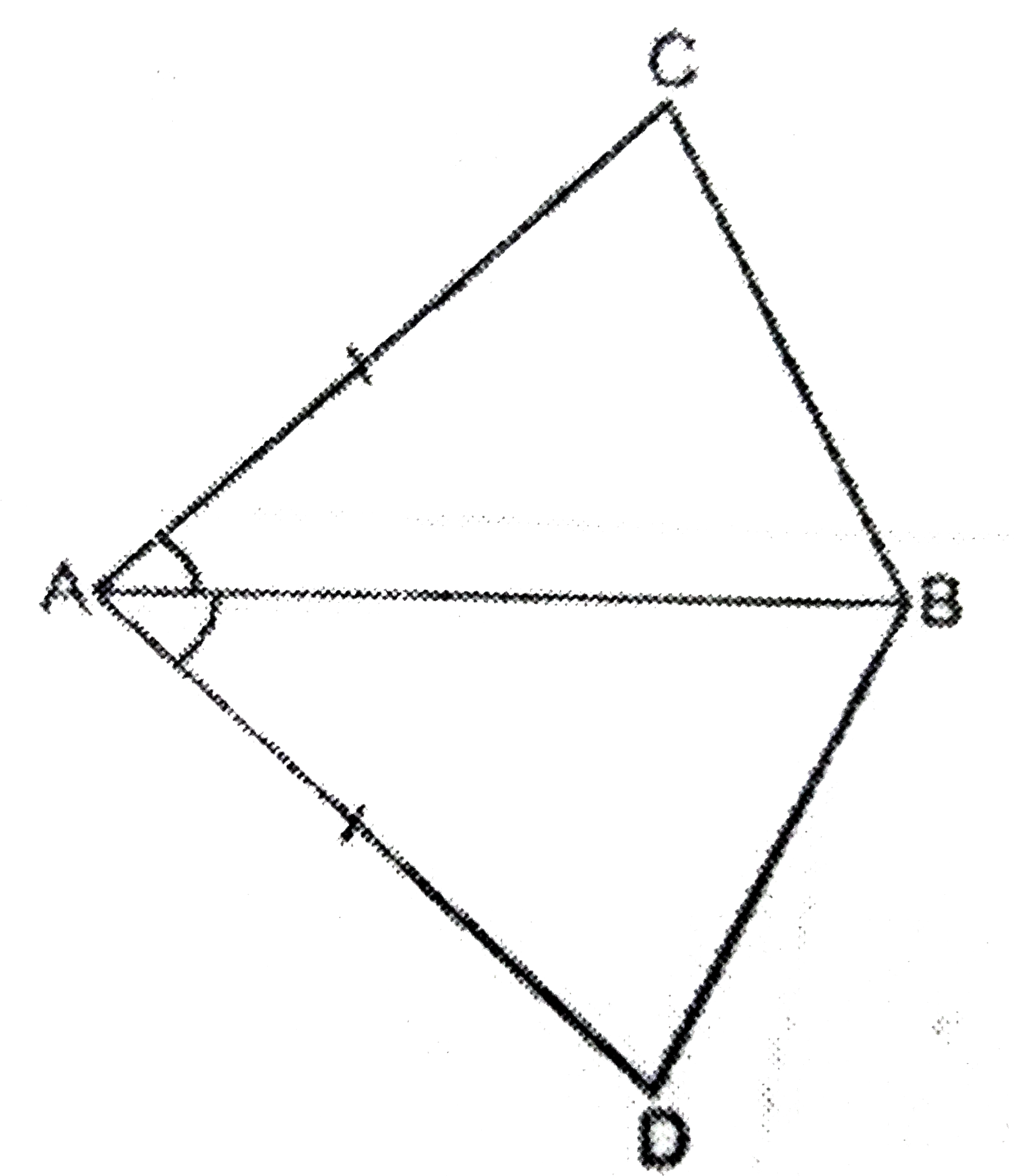
View Solutionएक समद्विबाहु त्रिभुज ABC में जिसमे AB=AC है ∠Bऔर∠C के समद्विबाजाक परस्पर बिंदु O पर प्रतिछेद करते है A और Oको जोड़िये दर्शाइए की
(i) OB=OC
(ii) AO कोण A समद्विभाजक करता है
View SolutionΔABC का ∠B समकोण है और भुजा AC का मध्य बिंदु P है। सिद्ध कीजिए कि
PB=PA=12AC
View Solutionनिम्नलिखित आलेख में से प्रत्येक आलेख के लिए दिए गए विकल्पों से सही समीकरण का चयन कीजिए।
आकृति के लिएआकृति के लिए(i)y=x(i)y=x+2(ii)x+y=0(ii)y=−x+2(iii)y=2x(iii)y=−x+2(iv)2+3y=7x(iv)x+2y=6

View SolutionStatement-1: 0<x<y⇒logax>logay, where a>1
Statement-2: Whena>1,logax is an increasing function.
View Solutionयदि किसी भी x>1,y>1और z>1 के लिए xln(yz)yln(xz)2zln(xy)=y4lny है, तो निम्नलिखित में से कौन-सा एक सही है
View Solutionआकृति में x>y तो सिद्ध करें की LM>LN
View SolutionIf x gt 1, y gt 1 , z gt 1 are in G.P then (1)/(1 + log x ), (1)/( 1 + log y ), (1)/(1 + log z) are in
View SolutionIf x>0, show that, x>log(1+x)>x−x22.
View SolutionIf x>0, show that,
x>log(x2+1)
View SolutionIf x>0, prove that,
x>log(1+x)>x1+x
View Solutionयदि x>1,y>1,z>1, गुणोत्तर श्रेढ़ी में हैं, तो 11+lnx,11+lny,11+lnz होंगे -
View SolutionIf x>1,y>1,z>1 are in G.P. , then 11+logx,11+logy and 11+logz are in
View SolutionIf x gt 1, y gt 1 , z gt 1 are in G.P., then : ( 1)/( 1+ log x ) , ( 1)/( 1+ log y ) , ( 1) /( 1 + log z ) are in :
View SolutionIf x gt 1, y gt 1, z gt 1 are in G.P then 1/(1 + log x),1/(1 + log y),1/(1 + log z) are in
View Solution
