Question

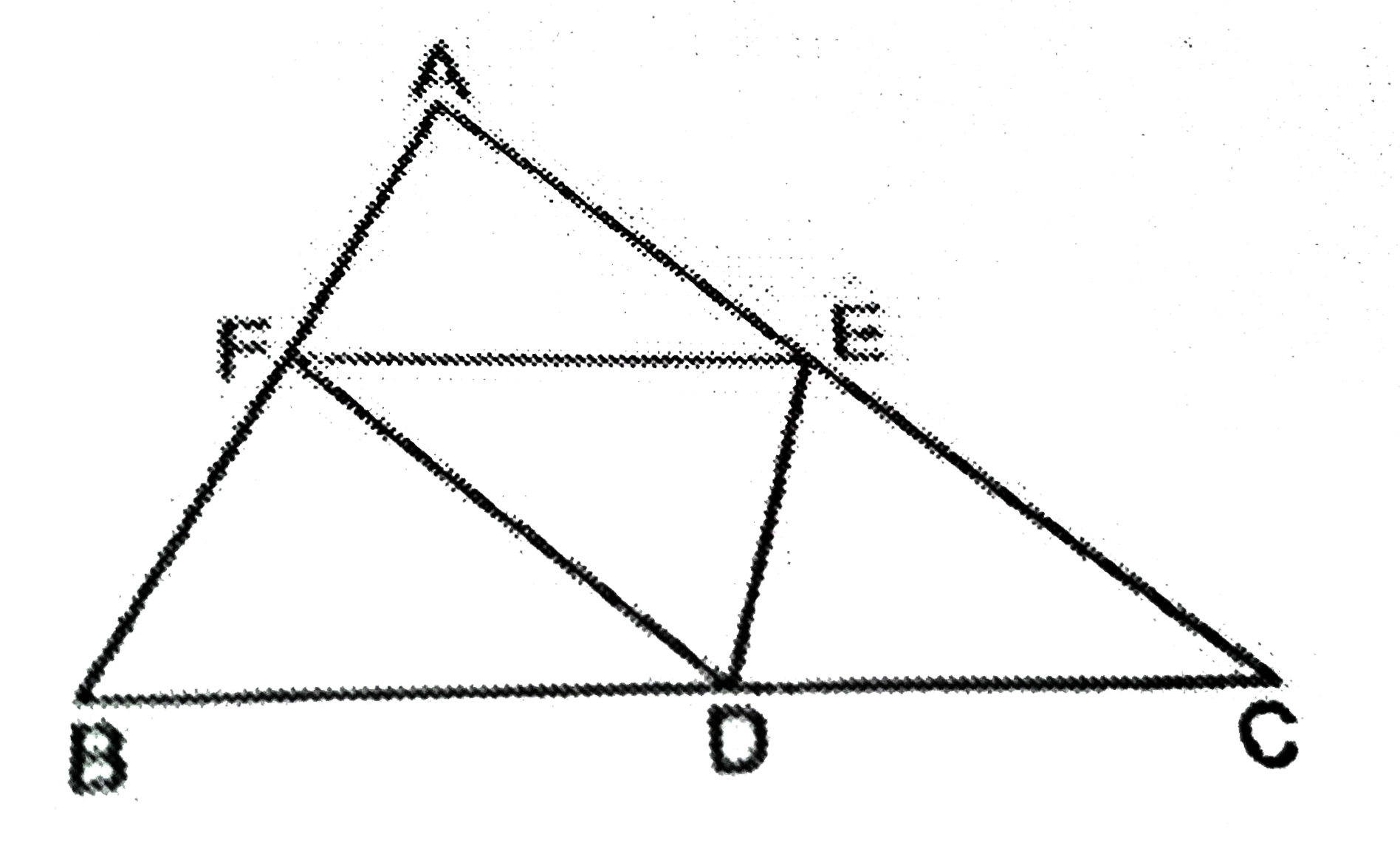
यदि D, E और F क्रमशः $\Delta ABC$ की भुजाओं BC, CA और AB के मध्य बिन्दु है। सिद्ध कीजिए कि BDEF एक समान्तर चतुर्भुज है जिसका क्षेत्रफल $\Delta ABC$ का आधा है। यह भी सिद्ध कीजिए कि
क्षे. $(\Delta DEF)=\frac{1}{4}$क्षे.(DeltaABC).

Explanation

विश्लेषण (Analysis) : DE, EF, तथा FD को मिला दें इससे `DeltaABC` चार छोटे त्रिभुजों में विभक्त हो गया। हमें यह दर्शाना है कि BDEF समान्तर चतुर्भुज है। क्या `FE||DB` तथा `ED||FB` पहले हम `FE||BD` को सिद्ध किया जा सकता है। तब `ED||FB` भी होगा। इस प्रकार BDEF समान्तर चतुर्भुज हो जाएगा। अब क्षेत्रफलों पर विचार करेंगे।
क्षे. (समा. चतु. BDEF ) = क्षे. `(DeltaBDF)+"क्षे."(DeltaDEF)`
परन्तु FD विकर्ण है, जिससे क्षे (समा चतु BDEF) = 2 क्षे. `(DeltaDEF)="क्षे. "(DeltaBDF)=" क्षे. "(DeltaDCE),=" क्षे. "(DeltaAFE)|DeltaABC`, चार छोटे त्रिभुजों से मिलकर बना है। अब हम उपपत्ति लिखेंगे।
उपपत्ति : `:'DeltaABC` में भुजा AB का मध्य बिन्दु F तथा भुजा AC का मध्य बिन्दु E है।
`:.FE||BD`
इसी प्रकार, `ED||FB" "......(1)
अतः BDEF समान्तर चतुर्भुज है।
`:'FD`, समान्तर चतुर्भुज BDEF का विकर्ण है। `:." क्षे."(DeltaFBD)=" क्षे. "(DeltaDEF)" "....(2)`
अब भुजाओ AC तथा BC के मध्य बिन्दु क्रमशः E और D है।
अतः उपर्युक्त के आधार पर
क्षे. `(DeltaEDC)="क्षे. "(DeltaDEF)" "....(3)`
ऐसी तर्क को F और D बिन्दुओ पर भी लगाकर
क्षे. `(DeltaAFE)="क्षे. "(DeltaEFD)" "....(4)`
`:'DeltaABC` चार अप्रतिच्छेती त्रिभुजों `DeltaAFE,DeltaDEF,DeltaBDF" और "DeltaDCE` में विभक्त है।
क्षे. `(DeltaABC)="क्षे. "(DeltaAFE)+"क्षे."(DeltaBDF)+"क्षे."(DeltaDCE)+"क्षे. "(DeltaDEF)`
समीकरण (2), (3), (4) और (5) से,
क्षे. `(DeltaABC)=4"क्षे. "(DeltaDEF)" "....(5)`
या क्षे. `(DeltaDEF)=(1)/(4)" क्षे. "(DeltaABC)" "....(6)`
समीकरण (2) व (6) से,
क्षे. (समा. चतु. BDEF )=क्षे. `(DeltaDEF)+"क्षे. "(DeltaFBD)`
`=2" क्षे. "(DeltaDEF)`
`2xx(1)/(4)"क्षे." (DeltaABC)`
`=(1)/(2)" क्षे. "(DeltaABC)" "...(7)`
हमें परिणाम (1), (7), व (6) ही सिद्ध करने थे ।