गोस नियम का उपयोग किये बिना किसी एक्शमन रेखिक आवेश घनत्व $λ$ के लम्बे पतले तार के कारण विधुत छेत्र के लिए सूत्र प्राप्त कीजिये संकेत शिंदे ही कलम नियम का उपयोग करके आवशयक समाकलन का मान निकालिये

Video Solution

Text Solution

Verified by Experts

रखिका आवेश घनात्मक $λ = \frac{d q}{d x}$

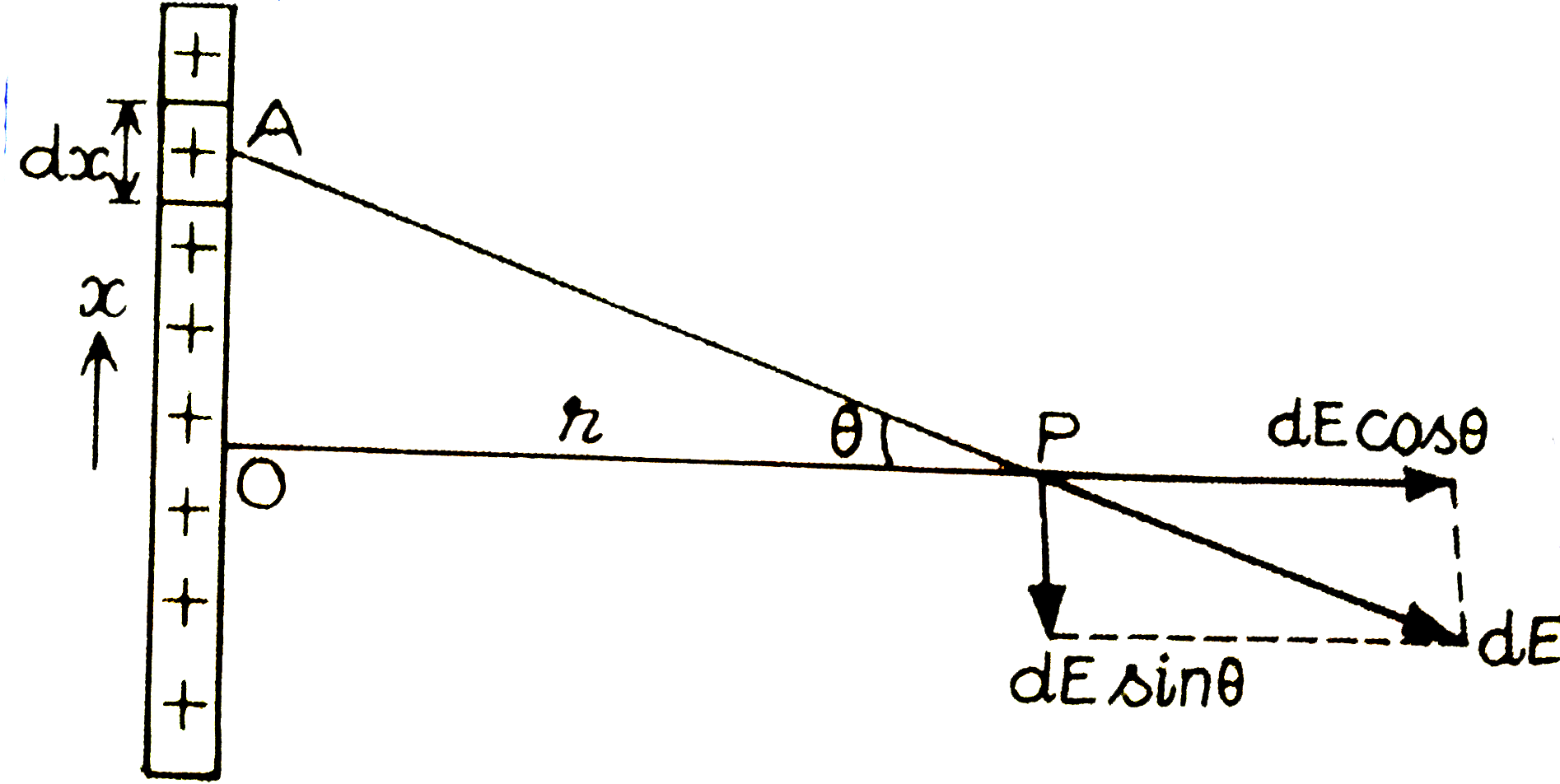
P पर विद्युत की त्रीवता $d E = \frac{1}{4 π ε_{0}} \frac{d q}{A p^{2}}$
माना $∠ O P A = θ$ तथा OP=r
विधुत क्षेत्र dE को OP के अनुदिशा तथा OP के लंबवत वियोजित करने पर
OP के अनुदिश घटक dE cos $θ$
OP के लाबवत घटक dE sin $θ$
OP के अनुदिश घटक परस्पर जुड़ा जबकि OP लंबवत घातक परस्पर निरस्त्र कर देंगे
अतः प्रभावित विधुत क्षेत्र $E = \int d E cos θ (- \infty) \int \infty \frac{1}{4 π ε_{0}} cos θ$
$A P = {(O P^{2} + O A^{2})}^{1 / 2}$
$= \frac{1}{4 π ε_{0}} \infty \int - \infty \frac{λ d x r}{{(x^{2} + r^{2})}^{3 / 2}}$
परन्तु $x = r tan θ$
$d x = r {sec}^{2} θ d θ$
$x = - \infty, θ = π / 2$
$x = + \infty, θ = π / 2$
$∴ E = \frac{1}{4 π ε_{0}} + π / 2 \int - π / 2 \frac{r^{2} {sec}^{2} θ d θ}{{(r^{2} {tan}^{2} θ + r^{2})}^{3 / 2}}$
$= \frac{1}{4 π ε_{0}} π / 2 \int - π / 2 \frac{1}{r} cos θ d θ$
$= \frac{1}{2 π ε_{0}} \frac{λ}{r}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

NOOTAN HINDI-वैधुत फ्लेक्स तथा गौस की प्रमेय -अतिरिक्त प्रशन

Home
Ask Doubt
Profile