एक वृत्ताकार कुण्डली जिसकी त्रिज्या 8.0 सेमी तथा फेरों की संख्या 20 है अपने ऊर्ध्वाधर व्यास के परितः 50रेडियन/सेकण्ड की कोणीय आवृत्ति से 3.0×10−2 टेस्ला के एकसमान चुम्बकीय क्षेत्र में घूम रही है । कुंडली में उत्पन्न अधिकतम तथा औसत प्रेरित विधुत वाहक बल का मान ज्ञात कीजिए । यदि कुण्डली 10Ω प्रतिरोध का एक बंद लूप बनाए तो कुण्डली में धारा के अधिकतम मान की गणना कीजिए। जूल उष्मन के कारण क्षयित औसत शक्ति की गणना कीजिए । यह शक्ति कहाँ से प्राप्त होती है ?
कुण्डली से बद्ध चुम्बकीय फ्लस्क
Φ=→B.→A=BAcosθ=BAcosωt (चूँकि θ=ωt)
कुण्डली से प्रेरित विo वाo बल,
e=−N'dθdt(BAcosωt)
=NBAωsinωt
अधिकतम प्रेरित विo वाo बल,
emax=NBAω=NB(πr2)ω
यहाँ N=20,r=8.0 सेमी =8.0×10−2 मीटर,B=3.0×10−2 टेस्ला ω=50रेडियन/सेकण्ड
∴emax=20×3.0×10−2×3.14×(8.0×10−2)2×50
e=0.603V.
औसत विo वाo बल, eav=NABω(sinωt)av=0
चूँकि पूरे चक्र के लिए sinωt का औसत मान शून्य होता है ।
अधिकतम प्रेरित धारा,
imax=emaxR=0.60310=0.0603A.
ऊष्मा के रूप में व्यय औसत शक्ति, Pmax=(i2)avR
अथवा Pmax=(e2)avR=12e2maxR
क्योकि पूरे चक्र के लिए sin2ωt का औसत मान 12 होता है । चूँकि
e2av=e2max2
∴Pmax=12×(0.603)210=0.018W
कुण्डली में प्रेरित धारा एक बल-आघूर्ण उत्पन्न करती है, जो कुण्डली के घूमने का विरोध करता है । इसलिए कुण्डली को एकसमान कोणीय वेग से घुमाया रखने के लिए एक बाह्य कारक (रोटर) बल-आघूर्ण प्रदान करता है । इसलिए व्यय ऊष्मा का स्रोत रोटर (rotor) हो है ।
Topper's Solved these Questions
- विद्युतचुम्बकीय प्रेरण BOOK - NOOTAN HINDICHAPTER - विद्युतचुम्बकीय प्रेरण EXERCISE - अतिरिक्त प्रश्न
7 Videos
- विद्युतचुम्बकीय प्रेरण BOOK - NOOTAN HINDICHAPTER - विद्युतचुम्बकीय प्रेरण EXERCISE - प्रश्नावली
21 Videos
- विद्युतचुम्बकीय प्रेरण BOOK - NOOTAN HINDICHAPTER - विद्युतचुम्बकीय प्रेरण EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न)
23 Videos
- रेडियोधर्मीताBOOK - NOOTAN HINDICHAPTER - रेडियोधर्मीताEXERCISE - वस्तुनिष्ठ प्रकार प्रशन
34 Videos
- विधुतचुम्बकीय तरंगे BOOK - NOOTAN HINDICHAPTER - विधुतचुम्बकीय तरंगे EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
12 Videos
Similar Questions
मान लीजिए की 6.4 अभ्यास में उलिलखित लूप स्थिर है किन्तु चुम्बकीय क्षेत्र उत्पन्न करने वाले विधुत चुम्बक में धारा का मान काम किया जाता है , जिससे चुम्बकीय क्षेत्र का मान अपने प्रारंभिक मान 0.3 टेस्ला से 0.2टेस्ला/सेकण्ड की दर से घटता है । अब यदि लूप का कटा भाग जोड़ दें जिससे प्राप्त बंद लूप का प्रतिरोध 1.6Ω हो तो इस लूप में ऊष्मन के रूप में शक्ति ह्यस क्या है ? इस शक्ति का स्रोत क्या है ?
View Solutionलेन्ज का नियम किसके सरंक्षण पर आधारित है ?
View Solutionकोई एकसमान चुम्बकीय क्षेत्र r त्रिज्या के किसी क्षेत्र में सीमित है । यह चुम्बकीय क्षेत्र समय के साथ d→B/dt की दर से परिवर्तित होता है । संलग्न आरेख के अनुसार, त्रिज्या R>r का लूप-1, r क्षेत्र को परिबद्ध करता है, तथा R त्रिज्या का लूप - 2, चुम्बकीय क्षेत्र की सीमा के बाहर है । उत्पन्न विo वाo बल का मान होगा :
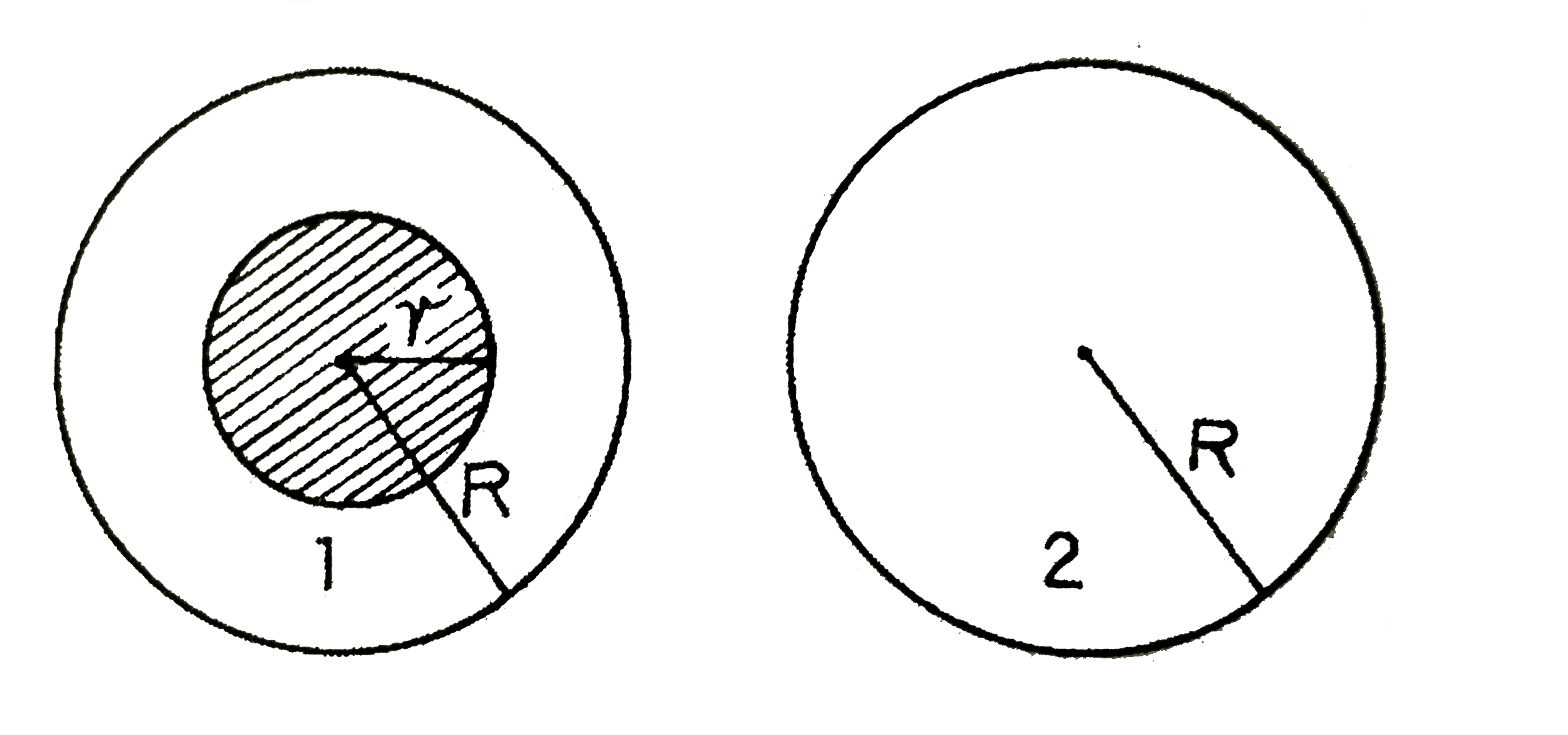
View Solutionएक रेडियोओएक्टीवे पदार्थ की वर्तमान गणन पर ( count rate ) 320 प्रति सेकण्ड है । 90 मिनट पश्चात् यह गिर क्र 40 प्रति सेकण्ड रह जाती है । पदार्थ की अर्द्ध - आयु है :
View Solutionदिए गए विकल्पों में किसका उपयोग एक संचरित विधुतचुम्बकीय तरंग उतपन्न करने में किया जा सकता है ?
View Solutionएक कुंडली को जिसका प्रेरण 0.50 तथा प्रतिरोध 100Ω है 240V व 50HZ की एक आपूर्ति से जोड़ा गया हैं | (a)कुंडली में अधिकतम धारा कितनी है? (b) वोल्टेज शीर्ष व् धारा शीर्ष के बीच समय-पश्चता कितनी है ?
यदि परिपथ को उच्च आवृत्ति की आपूर्ति ( 240 V , 10 kHz ) से जोड़ा जाता है तो अभ्यास 7.13 (a) तथा (b) के उत्तर निकालिए इसके इस कथन की व्याख्या कीजिए कि अति उच्च आवृत्ति पर किसी परिपथ में प्रेरक लगभग खुले परिपथ के तुल्य होता है स्थिर अवस्था के पश्चात किसी dc परिपथ में प्रेरक किस प्रकार का व्यवहार करता है
View Solution12 सेमी भुजा वाला वर्गाकार लूप जिसकी भुजाएँ X एवं Y अक्षो के समांतर है x - दिशा में 8 सेमी से−1 की गति से चलाया जा रहा है । लूप तथा उसकी गति का परिवेश धनात्मक z दिशा के चुम्बकीय क्षेत्र का है । चुम्बकीय क्षेत्र न तो एकसमान है और न ही समय के साथ नियत है । इस क्षेत्र की ऋणात्मक दिशा में प्रवणता 10−3" T सेमी"^(-1) है ( अर्थात ऋणात्मक X - दिशा में इकाई सेंटीमीटर दुरी पर क्षेत्र के मान में 10^(-3) T सेमी−1 की वृद्धि होती है ) तथा क्षेत्र के मान में 10−3" T से"^(-1)कीदरसेकमीभीहोरहीहै।तथाक्षेत्रकेमानमेंसेमीकीदरसेकमीभीहोरहीहै।यदिकुंडलीकाप्रतिरोध4.50 m Omega हो , तो प्रेरित धारा का परिणाम एवं दिशा ज्ञात कीजिए।
View SolutionE_("rms") = 100 वोल्ट का वि. वा. बल एक LCR श्रेणी परिपथ में लगाया गया है। यदि परिपथ में प्रेरणिक प्रतिघात, धारितीय प्रतिघात तथा प्रतिरोध के मान क्रमशः 4 ओम, 12 ओम तथा 6 ओम हों तो परिपथ के लिए निम्न का मान ज्ञात कीजिए-
वाट-हीन धारा का वर्ग माध्य मूल मान।
View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionएक शतरंज प्रतियोगिता में m पुरुष तथा दो महिलाएं भाग ले रही है । प्रत्येक प्रतिभागी (participant) दूसरे प्रत्येक प्रतिभागी के साथ दो गेम खेलता है । यदि पुरुषो के बीच आपस में खेले गए गेमों कि संख्या, पुरुष तथा महिलाओ के बीच खेले गए गेमों की संख्या से 84 अधिक है , तो m का मान है
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक बेलन का व्यास 10 सेमी. तथा ऊंचाई 7 सेमी. है, तो बेलन का आयतन ज्ञात कीजिए।
View Solutionनए की जन्म कुण्डली : एक पाठ के रचनाकार कौन हैं ?
View Solutionएक समान विधुत क्षेत्र में आवेशित कण की गति #!#वृत्ताकार वलय के कारण विधुत क्षेत्र की तीव्रता
View SolutionRecap|चल कुण्डली गैल्वेनोमीटर का अमीटर में रूपांतरण |चल कुण्डली गैल्वेनोमीटर का वोल्टमीटर में रूपांतरण
View Solution
