The x-coordiante of the incentre of the triangle that has the coordiantes of mid points of its sides as (0,1),(1,1) and (1,0) is:
2+√2
2−√2
1+√2
1−√2
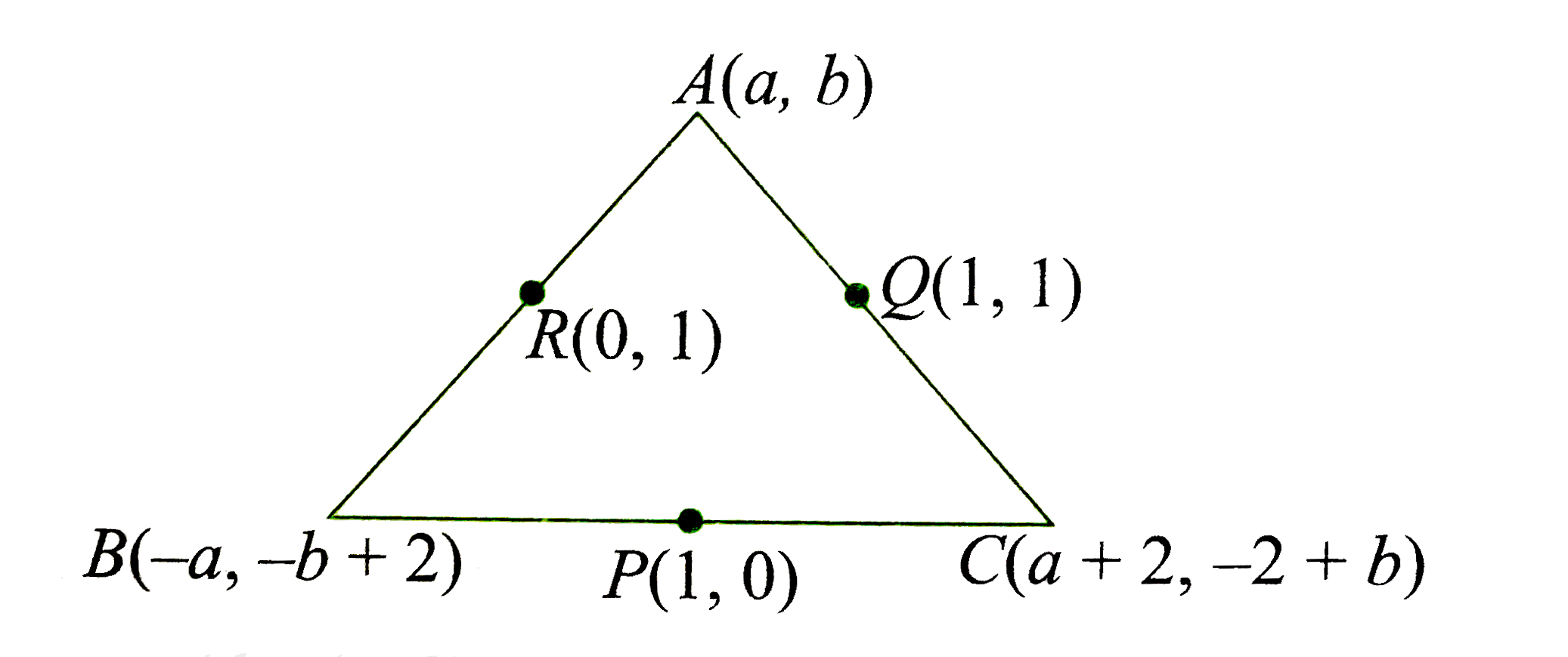
Let vertex A be (a, b).
R is mid point of AB.
∴B is (−a,−b+2)
Pis mid point of BC.
∴C is (a+2,−2+b)
Q is mid point of AC.
∴a=0 and b=2
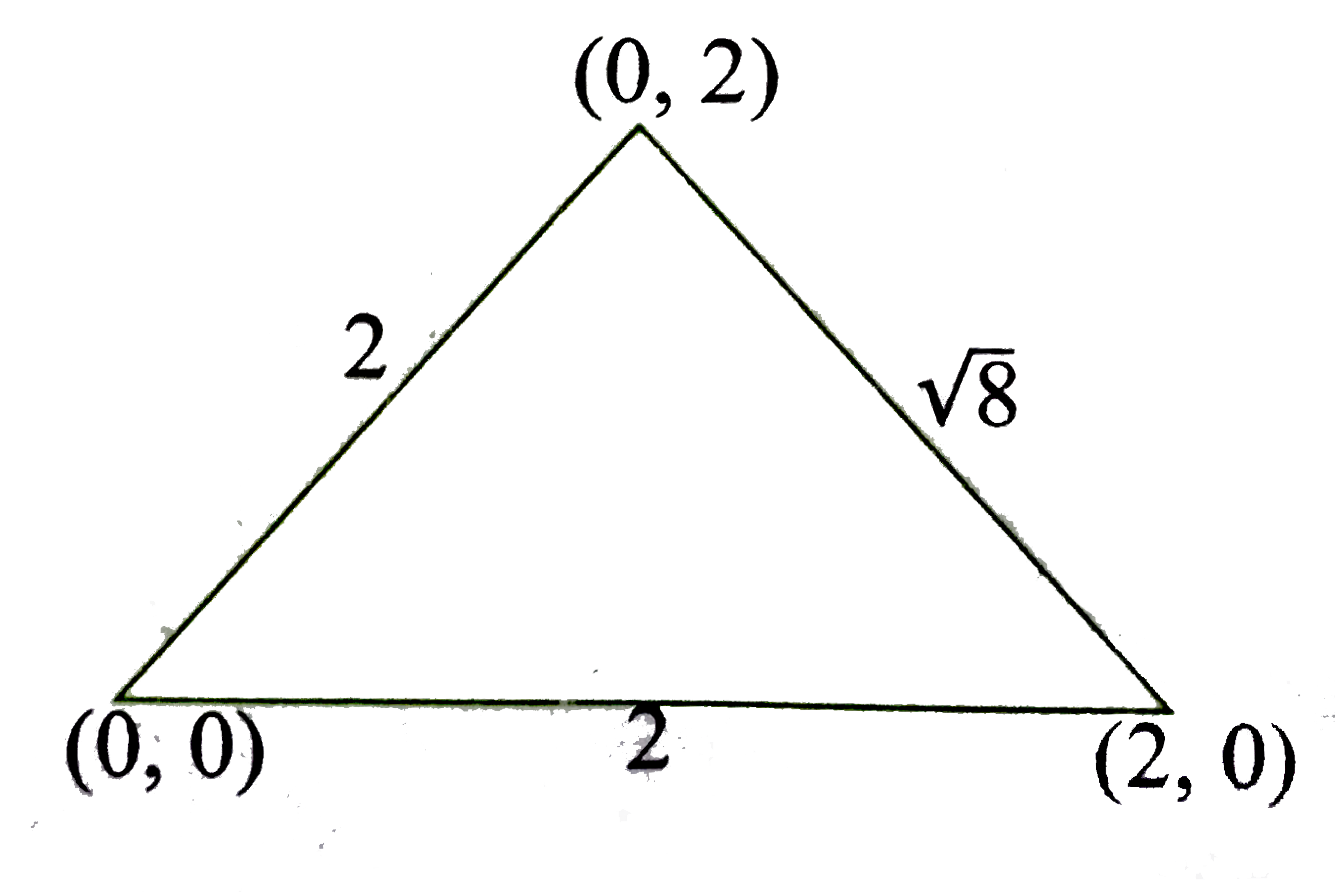
∴ Abscissa of in center
Ix=0×2+0×√8+2×22+2+2√2
∴Ix=44+2√2
⇒Ix=22+√2×2−√22−√2
⇒Ix=2(2−√2)2=2−√2
Similar Questions
The x-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as (0, 1), (1, 1) and (1, 0) is
View SolutionThe x-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as (0, 1), (1, 1) and (1, 0) is (1) 2−√2 (2) 1+√2 (3) 1−√2 (4) 2+√2
View Solution
Knowledge Check
The x -coordinate of the incentre of the triangle that has the coordinates of mid-points its sides are (0,1), (1,1) and (1, 0) is
A2+√2B2−√2C1+√2D1−√2The x -coordinate of the incentre of the triangle that has the coordinates of mid-points its sides are (0,1), (1,1) and (1, 0) is
A2+√2B2−√2C1+√2D1−√2The x-coordinates of the incentre of the triangle that has the coordinates of mid-point of its sides as (0, 1), (1, 1) and (1, 0), is
A2+√2B2−√2C1+√2D1−√2
Find the centroid of the triangle mid points of whose sides are (1,2,−3),(3,0,1)and(−1,1,4)
View SolutionFind the centroid of the triangle mid points of whose sides are (1,2,−3),(3,0,1)and(−1,1,4)
View SolutionFind the centroid of a triangle, mid points of whose sides are (1,2,-3), (3,0,1) and (-1,1,-4).
View SolutionFind the centroid of a triangle, mid points of whose sides are (1,2,-3), (3,0,1) and (-1,1,-4).
View SolutionThe incentre of the triangle with vertices (1,√3),(0,0) and (2,0) is
View Solution