In the figure, O is the center of the circle and BO is the bisector of angle ABC show that AB=BC
Video Solution
|
Answer
Step by step video & image solution for In the figure, O is the center of the circle and BO is the bisector of angle ABC show that AB=BC by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In the given figure, O is the centre of a circle and arc ABC subtends an angle of 130∘ at O. AB is extended to P, Then, ∠PBC is equal to
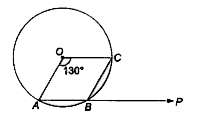 A25∘B40∘C65∘D75∘
A25∘B40∘C65∘D75∘In the given figure, ΔABC is inscribed in a circle and the bisector of ∠A meets BC in D and the circle in E. If ∠ECD=30∘, what is ∠A ?
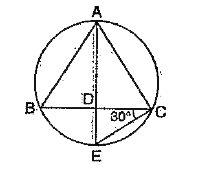 A60∘B45∘C70∘D150∘
A60∘B45∘C70∘D150∘In a circle with the centre is O and AB is the diameter of the circle and CD is the chord of the circle. If angle ABC is 54∘ and the length of CD and BC is equal, then find the ∠DBC.
A1. 36∘B2. 24∘C3. 48∘D4. 12∘
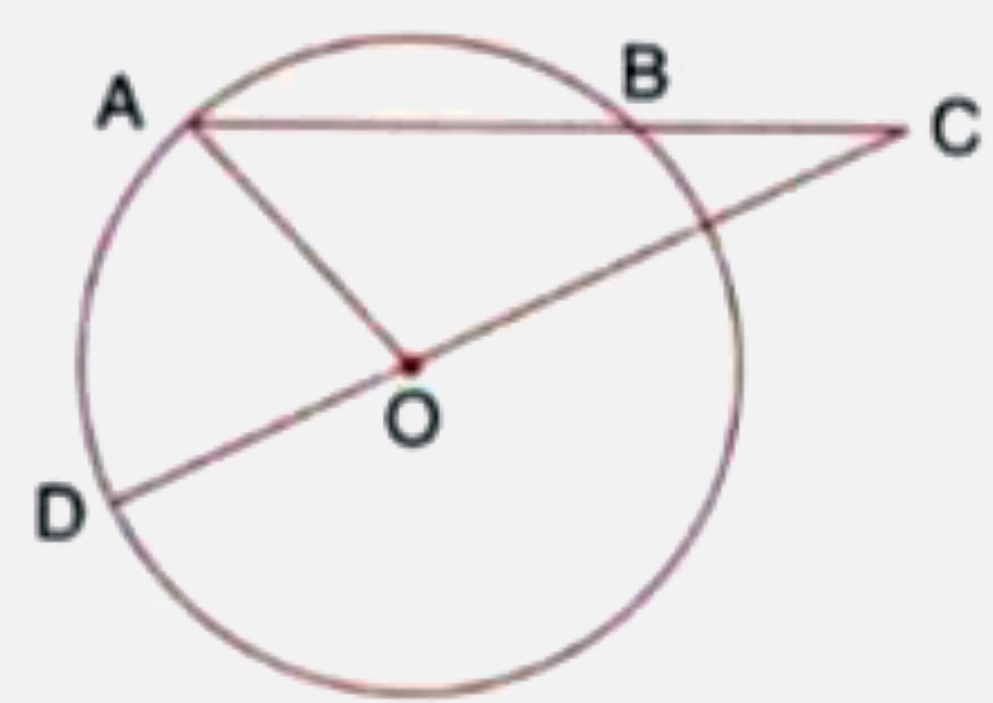
In the figure AB is the chord of a circle with centre O and DOC is a line segment such that BC=DO. If ∠C=20∘, find angle AOD.
View SolutionIn figure, ⌢AB≅⌢AC and O is the centre of the circle,Prove that OA is the perpendicualr bisector of BC.
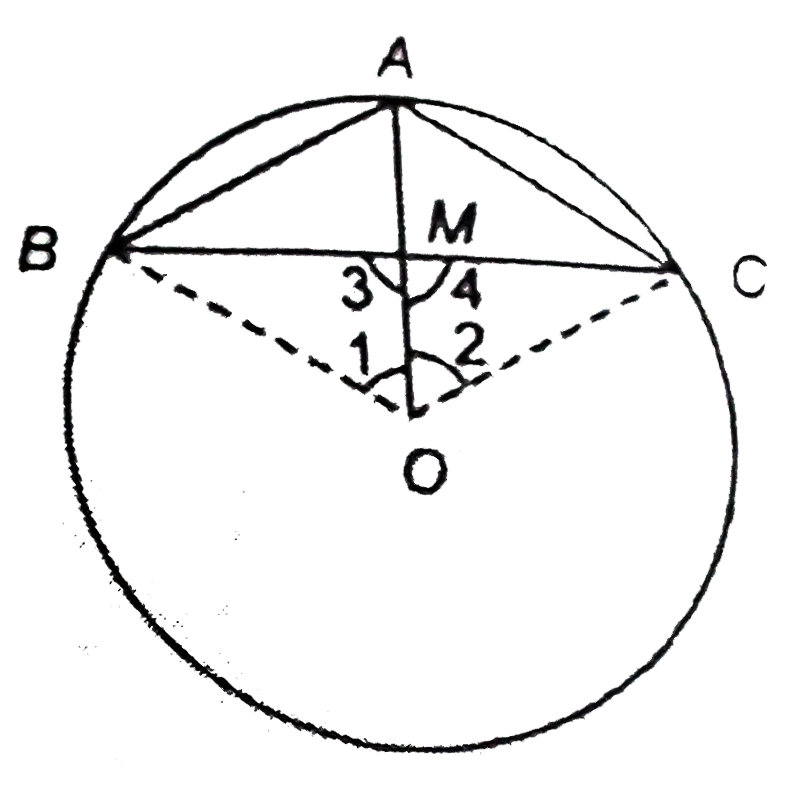
View SolutionIn figure, ⌢AB≅⌢AC and O is the centre of the circle,Prove that OA is the perpendicualr bisector of BC.

View SolutionIn Figure, ˆAB≅ˆAC and O is the centre of the circle. Prove that OA is the perpendicular bisector of BC
View SolutionIn the figure if EC is the bisector of ∠BCDandAB||CD||EF. Find ∠ABC
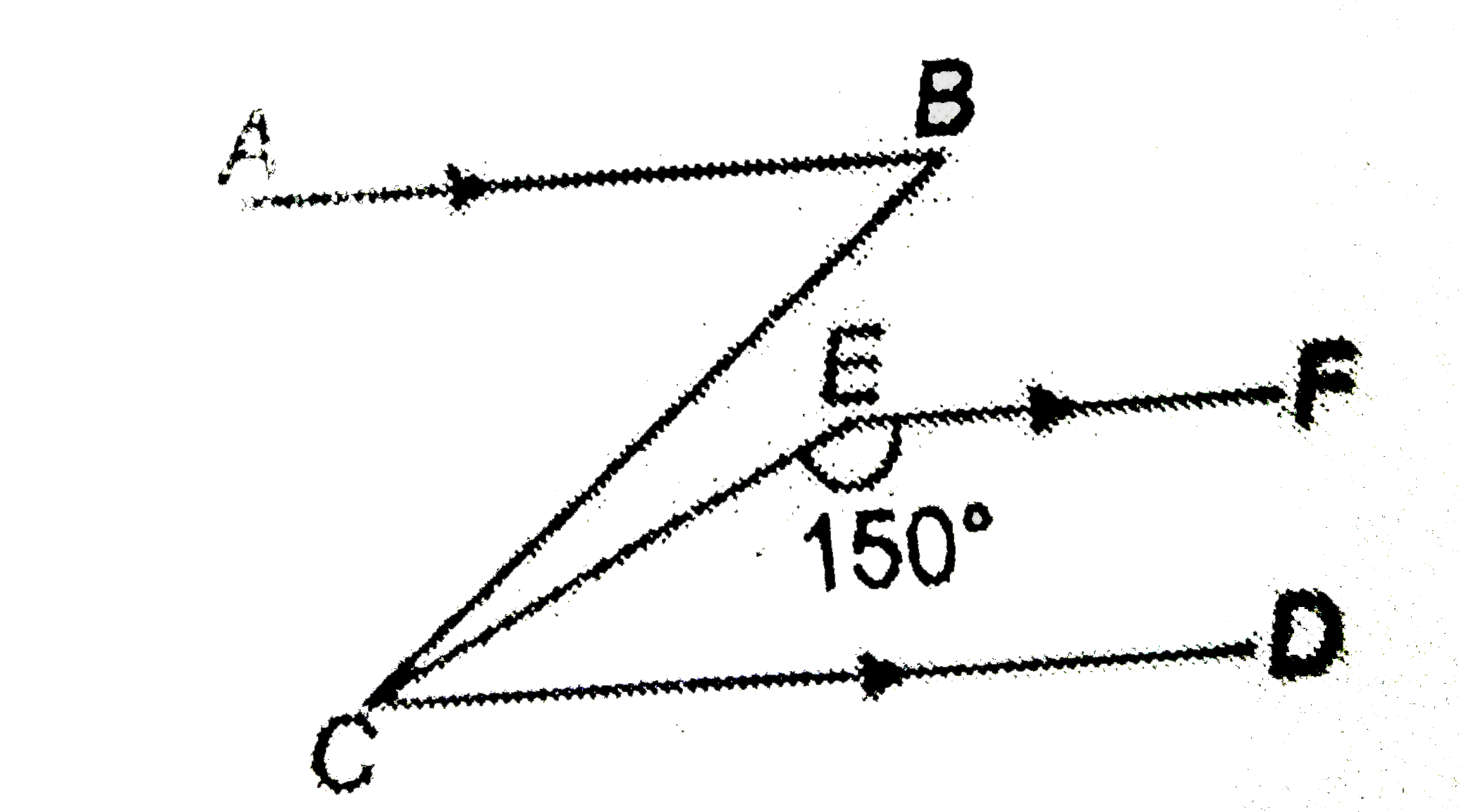
View Solution
