The horizontal cross-section of a water tank is in the shape of a rectangle with a semicircle at one end, as shown in fig. 18.20. The water is 2.4m deep in tank. Calculate the volume of the water in gallons.
Here, Area of water tank = Area of rectangle+ Area of semicircle
∴ Area of tank,A=(21∗7)+(12∗227∗72∗72)
A=147+774=166.25m2
As, water tank is 2.4 m deep in tank.
∴ Volume of tank, V=166.25∗2.4=399m3
Volume of tank in litres =399∗1000=399000
Volume of tank in gallons=3990003.78=105555.55 gallons
সম্পর্কিত প্রশ্ন
If the dimensions of water tank are 12.5 m, 4 m, 6 m, then the volume of water it can hold in litres is
View SolutionThe water for a factory is stored in a hemispherical tank whose internal diameter is 14 m. The tank contains 50 kL of water. Water is pumped into the tank to fill to its capacity. Calculate the volume of water pumped into the tank.
View Solution
জ্ঞান পরীক্ষা করুন
- Question 1 - Select One
Atank is 6km long,4m wide and 3/2m high.The volume of water in the tank is
A24m3B36m3C232m3D16m^3
The water for a factory is stored in a hemispherical tank whose internal diameter is 14 m. The tank contains 50 kL of water. Water is pumped into the tank to fill to its capacity. Calculate the volume of water pumped into the tank.
View SolutionA long cylindrical tank of cross-sectional area 0.5m2 is filled with water. It has a small hole at a height 50cm from the bottom. A movable piston of cross-sectional area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20kg is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)
 View Solution
View SolutionA long cylindrical tank of cross-sectional area 0.5m2 is filled with water. It has a small hole at a height 50cm from the bottom. A movable piston of cross-sectional area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20kg is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)
 View Solution
View SolutionThe length, breadth and height of a water tank are 5 m, 2.5 m and 1.25 m respectively. Calculate the capacity of the water tank in m3
View SolutionA long cylindrical tank of cross-section area 0.5m2 is filled with water. It has an opening at a height 50 cm from the bottom, having area of cross-section 1×10−4m2. A movable piston of cross-section area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20 kg is applied on the top of the water by piston, as shown in the figure. Find the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston). If this speed is (18x) m/s, find the value of x.
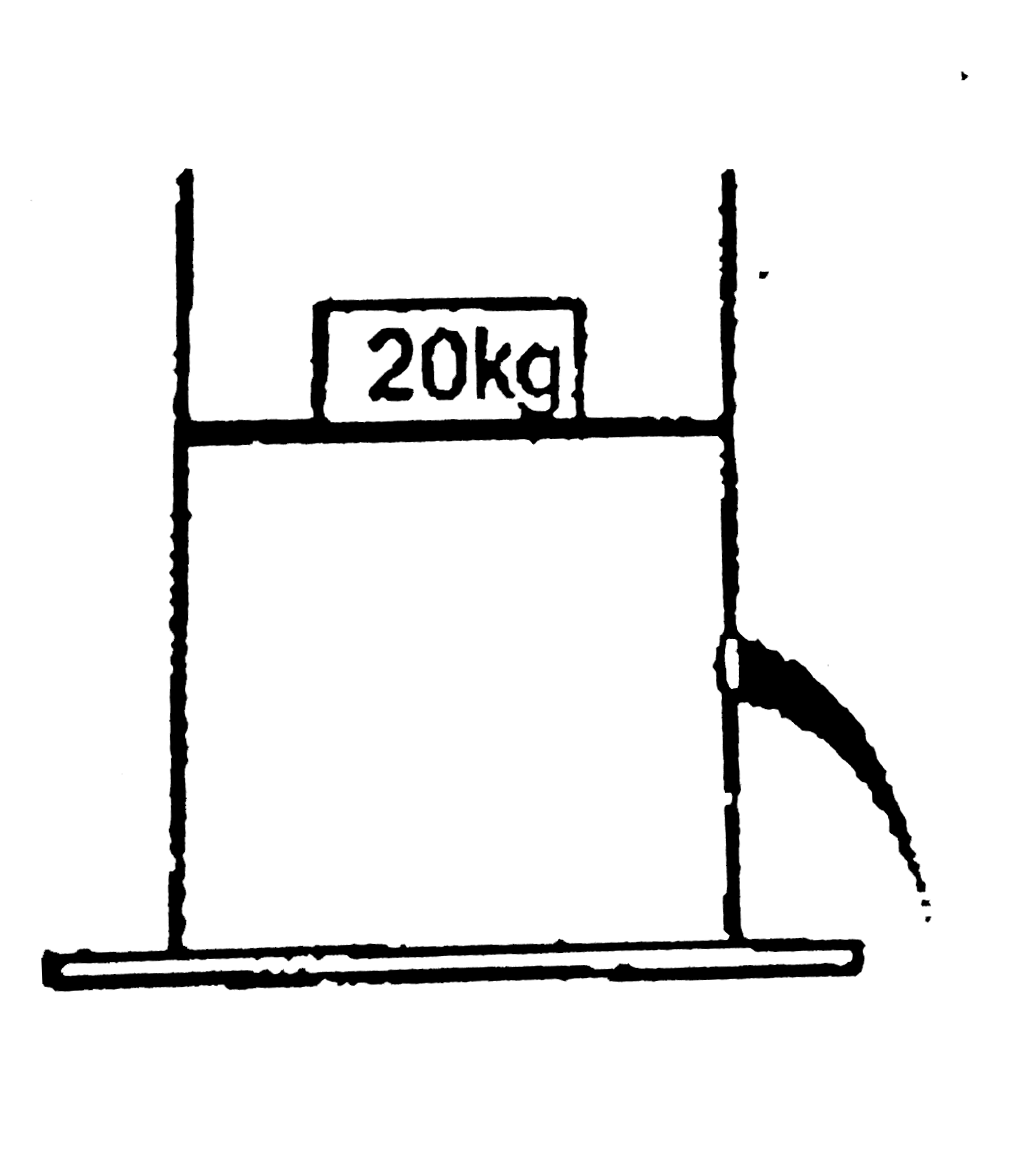 View Solution
View SolutionThe length, breadth and height of a water tank are 5 m, 2.5 m and 1.25 m respectively. Calculate the capacity of the water tank in litre
View SolutionA boat flaoting in a water tank is carrying a number of large stones. If the stones are unloaded into the water, what will happen to the water level in the tank
[ hint : Assume the initial level of the tank to be K and the length of the boat immersed in water to be h. Apply the law of floatition. find the volume of water in th tank. repeat the process after a plece of stone is unloaded. the stone will sink to the bottom .
assume the new height to be H' and h' respectively.
make use of the fact that the volume of water remains constant .
H−H=VA(PsPw−1)
where V = volume of stone , A = area of cross - section of tank , Ps = density of stone and Pw = desnsity of water .]View Solution

