Find angle θ, 0 < θ < π2 , which increase twice as fast as sine
Step by step video solution for Find angle theta, 0 < theta < pi/2 , which increase twice as fast as sine by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Find an angle θ,0<θ<π2, which increases twice as fast as its sine.
View SolutionFind an angle θ,0<θ<π2, which increases twice as fast as its sine.
View SolutionFind the angle θ,0<θ≤90∘,If
(i) sinθ=0.5373 (ii) cosθ=0.0087 (iii) cotθ=0.5750 (iv) logsinθ=−0.5.
View SolutionA body is thrown at an angle θ0 with the horizontal such that it attains a speed equal to (√23 times the speed of projection when the body is at half of its maximum height. Find the angle θ0.
View SolutionA body is thrown at an angle θ0 with the horizontal such that it attains a speed equal to √23 times the speed of projection when the body is at half of its maximum height. Find the angle θ0.
View SolutionThe system is in equilibrium. Find the angle θ
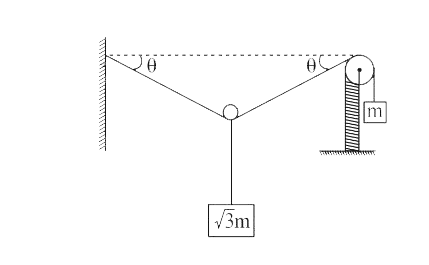
View SolutionThe system is in equilibrium. Find the angle θ

View SolutionAngle of a line with the positive direction of the x-axis is θ . The line is rotated about some point on it in anticlockwise direction by angle 450 and its slope becomes 3. Find the angle θ.
View SolutionIf 4sin2θ−1=0 and angle θ is less than 90∘, find the value of θ and hence the value of cos2θ+tan2θ.
View SolutionIf 4sin2θ−1=0 and angle θ is less than 90∘, find the value of θ and hence the value of cos2θ+tan2θ.
View Solution