ABC is any triangle. P is the mid-point of BC,Q is the mid-point of CAand R is the mid-point of AB. The expression −−→AP+−−→BQ+−−→CR equals
Step by step video & image solution for ABC is any triangle. P is the mid-point of BC,Q is the mid-point of CAand R is the mid-point of AB. The expression vec(AP) +vec(BQ) +vec(CR) equals by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
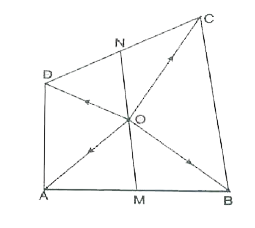
In the figure, M is the mid - point of [AB] and N is the mid - point of [CD] and O is the mid - point of [MN]. Prove that :
(i) −−→OA+−−→OB+−−→OC+−−→OD=→0
(ii) −−→BC+−−→AD=2−−−→MN.
View SolutionIn figure, P is the mid-point of BC,,Q is the mid-point of AP , such that BQ produced meets AC at R. Prove that 3RA=CA
View Solution
Knowledge Check
In ΔABC, P is a point on BC such that BP:PC=4:5 and Q is the mid - point of BP. Then area (ΔABQ) : area (ΔABC) is equal to :
A1:3B1:9C2:9D2:5D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC and G is the centroid of the triangle, then −−→GD+−−→GE+−−→GF=
A→0B2−−→ABC2−−→GAD2−−→GC
D is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionIn triangle ABC, M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use Intercept Theorem to show that MN bisects AD.
View SolutionIf P, Q , R are the mid-points of the sides AB, BC and CA of ΔABC and O is point whithin the triangle, then −−→OA+−−→OB+−−→OC=
View SolutionD is the mid-point of side BC of ΔABC and E is the mid-point of BO. If O is the mid-point of AE, then ar(ΔBOE) = 1/k ar(ΔABC). Then k equals
View SolutionIf D is the mid-point of the side BC of a triangle ABC, prove that →AB+→AC=2→AD.
View Solution
