In the given figure ΔABC is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of ΔABC, r1 as the radius of incircle ΔPAC and r2 as the ex-radius of ΔPBC with respect to side BC. Then r1+r2 is equal to
Step by step video & image solution for In the given figure DeltaABC is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of DeltaABC, r_1 as the radius of incircle DeltaPAC and r_2 as the ex-radius of DeltaPBC with respect to side BC. Then r_1 + r_2 is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023সম্পর্কিত প্রশ্ন
In the given figure ΔABC is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of ΔABC, r1 as the radius of incircle ΔPAC and r2 as the ex-radius of ΔPBC with respect to side BC. Then r1+r2 is equal to
View SolutionIn the given figure, ΔABC is an equilateral triangle whose side BC has been produced in both the directions to D and E respectively. Prove that ∠ACD=∠ABE.
View Solution
জ্ঞান পরীক্ষা করুন
The incircle of ΔABC touches side BC at D. The difference between BD and CD (R is circumradius of ΔABC) is
A∣∣∣4Rsin.A2sin.B−C2∣∣∣B∣∣∣4Rcos.A2sin.B−C2∣∣∣C|b−c|D∣∣∣b−c2∣∣∣
If ΔABC is a equilateral triangle and P, Q, R are mid-points of sides AB, BC and CA respectively then-
View SolutionThe incircle of ΔABC touches side BC at D. The difference between BD and CD (R is circumradius of ΔABC) is
View SolutionIn the given figure ABCD is a trapezium, P is the mid-point of side AD and PR||AB||DC.
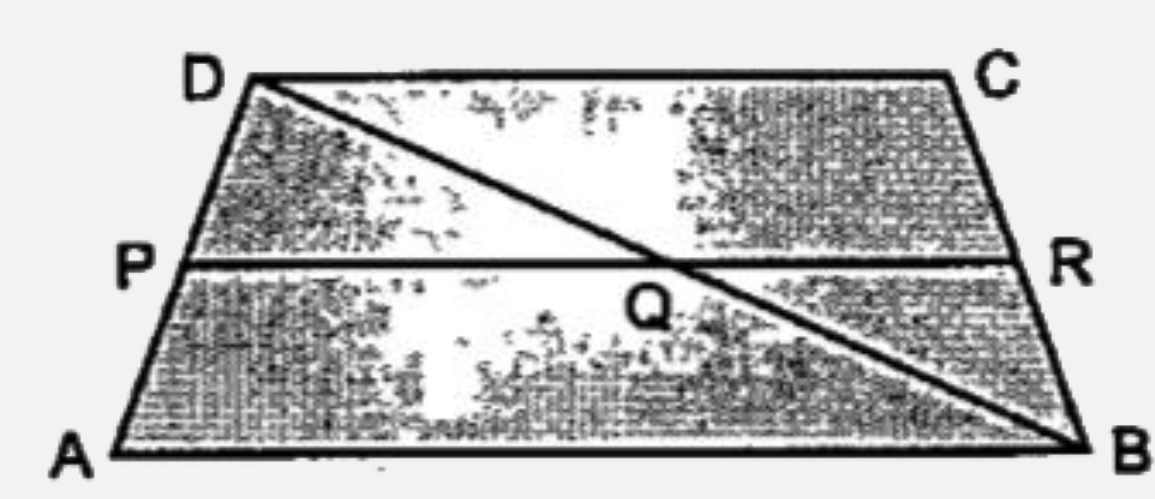
Prove that R is the mid-point of side BC
View SolutionLet the centroid of an equilateral triangle ABC be at the origin. Let one of the sides of equilateral triangle be along the straight line x+y=3. If R and r be the radius of circumcircle and incircle respectively of △ABC, then (R+r) is equal to :
View SolutionLet ABC be an equilateral triangle with side length a. Let R and r denote the radii of the circumcircle and the incircle of triangle ABC respectively. Then, as a function of a, the ratio Rr
View Solution
If a circle touches the side BC at point P, extended side AB at Q and extended side AC at R. Then AQ is equal to :
View SolutionIn ΔABC ,with usual notations r1,r2,r3 are in harmonic progression. If area of ΔABC is 24 and perimeter is 24 then length of its sides are
View Solution
