Two particles of same mass 'm' moving with velocities →v1=vˆi,and→v2=(v2)ˆi+(v2)ˆjcollide in-elastically. Find the loss in kinetic energy
√23mu2
34mu2
13mu2
18mu2
The correct Answer is:4
Step by step video & image solution for Two particles of same mass 'm' moving with velocities vecv_1= vhati, and vecv_2 = (v/2)hati + (v/2)hatjcollide in-elastically. Find the loss in kinetic energy by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two particles of mass 2m and m moving with speed v and 2v respectively perpendicular to each other collides perfectly inelastically, then
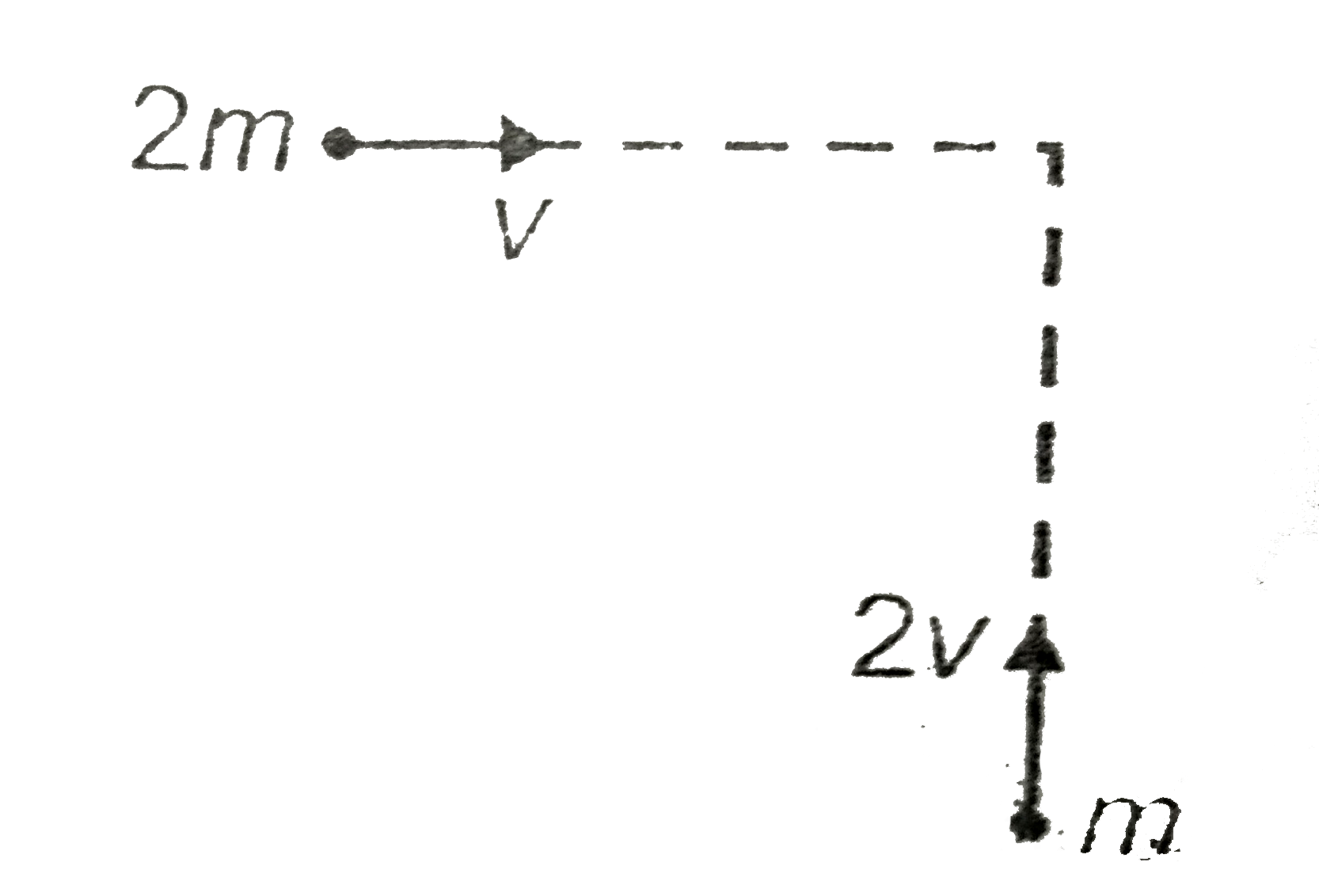
Loss in kinetic energy of the system
View SolutionA particle of mass m moving with velocity 2v collides with another particle of mass 3m moving with velocity v in the same direction.If it is perfect inelastic collision,the loss of kinetic energy of the system is
View Solution
Knowledge Check
Two particles of same mass m moving with velocities u1 and u2 collide perfectly inelastically. The loss of energy would be :
A1/2m(u1−u2)2B1/4m(u1−u2)2Cm(u1−u2)2D2m(u1−u2)2Two perfectly elastic balls of same mass m are moving with velocities u1 and u2. They collide elastically n times. The kinetic energy of the system finally is:
A12m∪21B12mu(u21+u22)C12m(u21+u22)D12mn(u21+u22)Two particles of equal mass m are moving with velocities vˆi and v(ˆi+ˆj2) respectively. If the particles collide completely inelastically, then the energy lost in the process is
A3mv24B2mv23Cmv23Dmv28
Two objects having same mass 'm' are moving with velocities v and 2v. Find ratio of their kinetic energies.
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Find the angle with the horizontal to which the particles move after collision.
View SolutionTwo identical mass M moving with velocity u1andu2 collide perfectly inelastically. The loss in kinetic energy is
View SolutionTwo particles of masses m1andm2 in projectile motion have velocities →v1and→v2 respectively at time t=0. They collide at time t0. Their velocities become →v1'and→v2' at time 2t0 while still moving in air. The value of |(m1→v1'+m2→v2')−(m1→v1+m2→v2)| is
View SolutionA particle of mass 1 g moving with a velocity →v1=3ˆi−2ˆj ms−1 experiences a perfectly in elastic collision with another particle of mass 2 g and velocity →v2=4ˆj−6ˆk ms−1. The velocity of the particle is
View Solution
