i+i2+i3+i4
Step by step video & image solution for i+i^2+i^3+i^4 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Find the values of following expressions: i49+i68+i89+i110 (ii) i30+i80+i120 (iii) i+i2+i3+i4 (iv) i5+i10+i15 (v) i592+i590+i586+i584i582+i580+i576+i574 (vi) 1+i2+i4+i6+i8+.i20 (vii) (1+i)6+(1−i)3
View SolutionFind the value of i2+i4+i6+i71+i2+i3 is
( a ) 1−i
( b ) 1+i
( c ) 2−i
( d ) 2+iView Solution
Knowledge Check
- Question 1 - Select One
12i2−4i3+8i4−4i5=?
A1B2C4D−4
Find the modulus and argument of the complex number z=i2+i3i4+i5
View SolutionThe value of i0+i1+i2+i3+i4 is
View SolutionEvaluate 2i2+6i3+3i16−6i19+4i25
View Solutionif z=2+i+4i2−6i3 then verify that
(i) (¯¯¯¯z2=(¯z)2)View SolutionFind relation in between current i1,i2,i3,i4,i5 and i6.
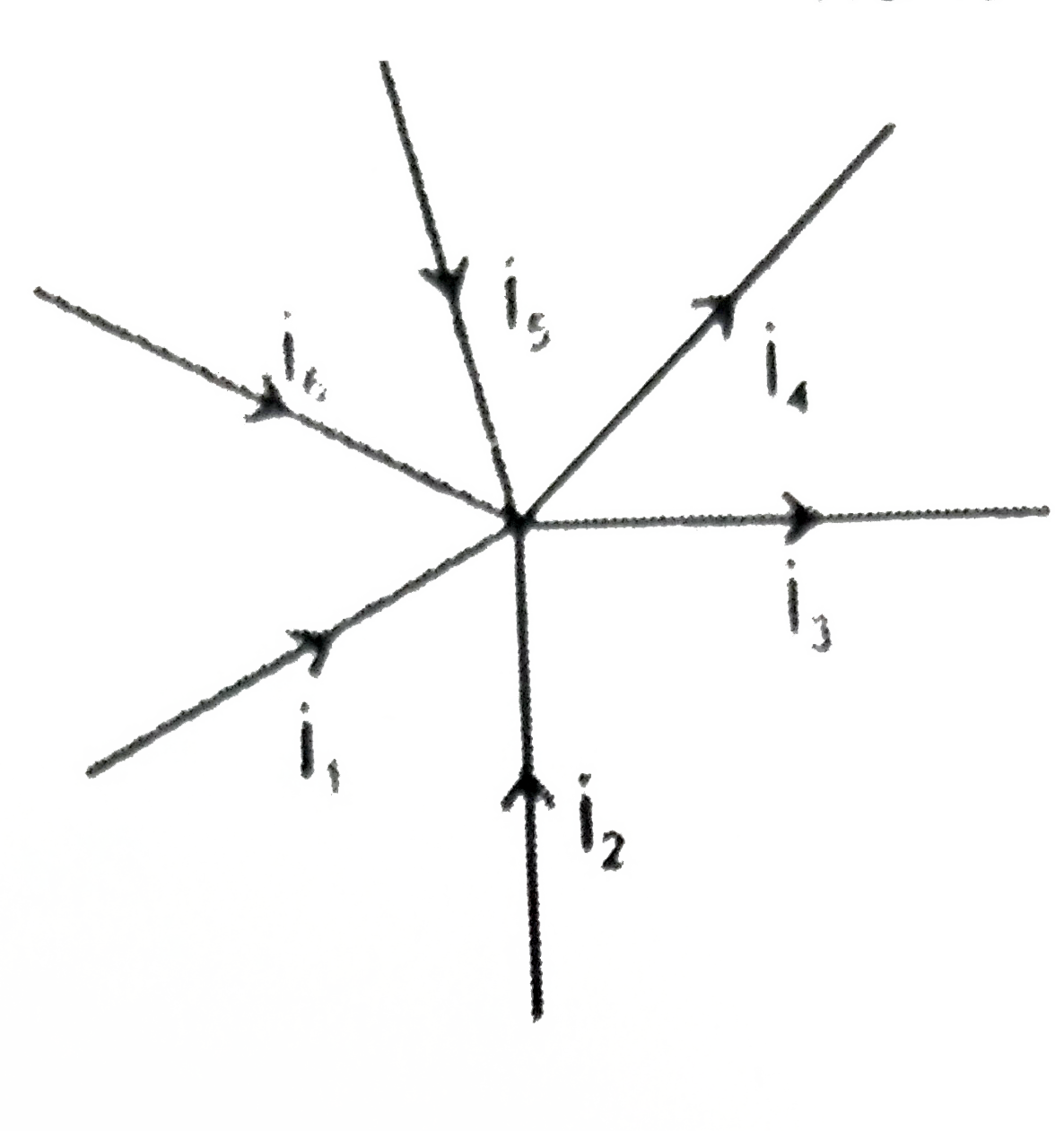 View Solution
View SolutionWrite the following in the form x+iy:
(i) (3+2i)(2−i)
(ii) 2i2+6i3+3i16−6i19+4i25.
(iii) (3−2i)(2+3i)(1+2i)(2−i).View SolutionEvaluate: i2+i4+i6+i71+i2+i3
View Solution
