There are 15 points in a plane, no three of which are in the same straight line with the exception of 6, which are all in the same straight line. Find the number of i. straight lines formed, ii. number of triangles formed by joining these points.
Step by step video & image solution for There are 15 points in a plane, no three of which are in the same straight line with the exception of 6, which are all in the same straight line. Find the number of i. straight lines formed, ii. number of triangles formed by joining these points. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
There are 10 points in a plane, no three of which are in the same straight line excepting 4, which ane collinear. Then, number of (A) straight lines formed by joining them is 40 (B) triangles formed by joining them is 116(C) straight lines formed by joining them is45 (D) triangles formed by joining them is 120
View SolutionThere are 10 points in a plane, no three of which are in the same straight line, except 4 points, which are collinear.
Find (i) the number of lines obtained from the pairs of these points,
(ii) the number of triangles that can be formed with vertices as these points.
View Solution
Knowledge Check
There are n points in a plane no three of which are in the same straight line with the exception of m(n>m)points which are all in the same straight line. Find the number of triangles formed by joining them.
An−mC3BnC3−mC3CnCmDnone of (a),(b ),(c )There are 15 points in a plane, no three of which are in a straight line except 4, all of which are in a straight line. The number of triangles that can be formed by using these 15 points is:
A404B415C451D490There are 15 points in a plane, no two of which are in a straight line except 4, all of which are in a straight line. The number of triangles that can be formed by using these 15 points is
A404B415C451D490
There are ten points in a plane. Of these ten points, four points are in a straight line and with the exceptionof these four points, on three points are in the same straight line. Find i. the number of triangles formed, ii the number of straight lines formed iii the number of quadrilaterals formed, by joining these ten points.
View SolutionThree are 12 points in a plane, no of three of which are in the same straight line, except 5 points whoich are collinear. Find
(i) the numbers of lines obtained from the pairs of these points.
(ii) the numbers of triangles that can be formed with vertices as these points.
View SolutionFind the number of straight lines and the number of triangles in the complex figure given below .
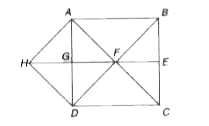
View SolutionThere are 10 points in a plane, out of these 6 are collinear. The number of triangles formed by joining these points, is
View SolutionIf 7 points out of 12 are in the same straight line, then what is the number of triangles formed?
View Solution
